
【题目】已知函数f(x)=x3﹣ax2+bx+c(a,b,c∈R).
(1)若函数f(x)在x=﹣1和x=3处取得极值,试求a,b的值;
(2)在(1)的条件下,当x∈[﹣2,6]时,f(x)<2|c|恒成立,求c的取值范围.
【答案】(1)![]() ; (2)(-∞,-18)∪(54,+∞).
; (2)(-∞,-18)∪(54,+∞).
【解析】
(1)根据函数的极值的概念得到方程组解出参数值即可;(2)对函数求导得到函数的单调性和极值,进而得到函数的最大值为c+54,要使f(x)<2|c|恒成立,只要c+54<2|c|即可.
(1)f′(x)=3x2-2ax+b,
∵函数f(x)在x=-1和x=3处取得极值,
∴-1,3是方程3x2-2ax+b=0的两根.
∴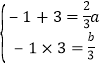 ∴
∴![]() .
.
经检验满足题意.
(2)由(1)知f(x)=x3-3x2-9x+c,
f′(x)=3x2-6x-9.令f′(x)=0,得x=-1或x=3.
当x变化时,f′(x),f(x)随x的变化情况如下表:
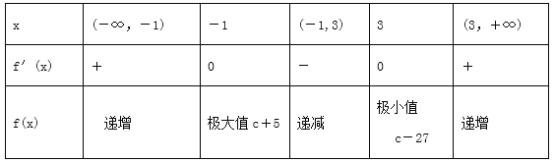
而f(-2)=c-2,f(6)=c+54,
∴当x∈[-2,6]时,f(x)的最大值为c+54,
要使f(x)<2|c|恒成立,只要c+54<2|c|即可,
当c≥0时,c+54<2c,∴c>54 ,
当c<0时,c+54<-2c,∴c<-18.
∴c∈(-∞,-18)∪(54,+∞),此即为实数c的取值范围.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】如图,分别过椭圆![]() 左、右焦点
左、右焦点![]() 的动直线
的动直线![]() 相交于
相交于![]() 点,与椭圆
点,与椭圆![]() 分别交于
分别交于![]() 与
与![]() 不同四点,直线
不同四点,直线![]() 的斜率
的斜率![]() 满足
满足![]() .已知当
.已知当![]() 与
与![]() 轴重合时,
轴重合时,![]() ,
,![]() .
.
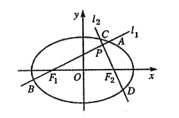
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出
为定值?若存在,求出![]() 点坐标并求出此定值;若不存在,说明理由.
点坐标并求出此定值;若不存在,说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,
,![]() 和
和![]() .
.
【解析】试题分析:(1)当![]() 与
与![]() 轴重合时,
轴重合时,![]() 垂直于
垂直于![]() 轴,得
轴,得![]() ,得
,得![]() ,
,![]() 从而得椭圆的方程;(2)由题目分析如果存两定点,则
从而得椭圆的方程;(2)由题目分析如果存两定点,则![]() 点的轨迹是椭圆或者双曲线 ,所以把
点的轨迹是椭圆或者双曲线 ,所以把![]() 坐标化,可得
坐标化,可得![]() 点的轨迹是椭圆,从而求得定点
点的轨迹是椭圆,从而求得定点![]() 和点
和点![]() .
.
试题解析:![]() 当
当![]() 与
与![]() 轴重合时,
轴重合时,![]() , 即
, 即![]() ,所以
,所以![]() 垂直于
垂直于![]() 轴,得
轴,得![]() ,
,![]() ,, 得
,, 得![]() ,
,![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
![]() 焦点
焦点![]() 坐标分别为
坐标分别为![]() , 当直线
, 当直线![]() 或
或![]() 斜率不存在时,
斜率不存在时,![]() 点坐标为
点坐标为![]() 或
或![]() ;
;
当直线![]()
![]() 斜率存在时,设斜率分别为
斜率存在时,设斜率分别为![]() , 设
, 设![]()
![]() 由
由 , 得:
, 得:
![]() , 所以:
, 所以:![]() ,
,![]() , 则:
, 则:
![]()
![]() . 同理:
. 同理:![]()
![]() , 因为
, 因为
![]() , 所以
, 所以![]()
![]() , 即
, 即![]() , 由题意知
, 由题意知![]() , 所以
, 所以
![]() , 设
, 设![]() ,则
,则![]() ,即
,即![]() ,由当直线
,由当直线![]() 或
或![]() 斜率不存在时,
斜率不存在时,![]() 点坐标为
点坐标为![]() 或
或![]() 也满足此方程,所以点
也满足此方程,所以点![]() 在椭圆
在椭圆![]() 上.存在点
上.存在点![]() 和点
和点![]() ,使得
,使得![]() 为定值,定值为
为定值,定值为![]() .
.
考点:圆锥曲线的定义,性质,方程.
【方法点晴】本题是对圆锥曲线的综合应用进行考查,第一问通过两个特殊位置,得到基本量![]() ,
,![]() ,得
,得![]() ,
,![]() ,从而得椭圆的方程,第二问由题目分析如果存两定点,则
,从而得椭圆的方程,第二问由题目分析如果存两定点,则![]() 点的轨迹是椭圆或者双曲线 ,本题的关键是从这个角度出发,把
点的轨迹是椭圆或者双曲线 ,本题的关键是从这个角度出发,把![]() 坐标化,求得
坐标化,求得![]() 点的轨迹方程是椭圆
点的轨迹方程是椭圆![]() ,从而求得存在两定点
,从而求得存在两定点![]() 和点
和点![]() .
.
【题型】解答题
【结束】
21
【题目】已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的极值;
的极值;
(Ⅱ)若函数![]() 的两个零点为
的两个零点为![]() ,记
,记![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在△ABC中,角A、B、C的对边分别是a、b、c,且2sin2A+3cos(B+C)=0.
(1)求角A的大小;
(2)若△ABC的面积S=![]() ,求sinB+sinC的值.
,求sinB+sinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣1+alnx.(e为自然对数的底数),λ=min{a+2,5}.(min{a,b}表示a,b中较小的数.)
(1)当a=0时,设g(x)=f(x)﹣x,求函数g(x)在[![]() ,
,![]() ]上的最值;
]上的最值;
(2)当x![]() 1时,证明:f(x)+x2
1时,证明:f(x)+x2![]() λ(x﹣1)+2.
λ(x﹣1)+2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔业公司今年初用98万元购进一艘远洋渔船,每年的捕捞可有50万元的总收入,已知使用![]() 年(
年(![]() )所需(包括维修费)的各种费用总计为
)所需(包括维修费)的各种费用总计为![]() 万元.
万元.
(1)该船捞捕第几年开始赢利(总收入超过总支出,今年为第一年)?
(2)该船若干年后有两种处理方案:
①当赢利总额达到最大值时,以8万元价格卖出;
②当年平均赢利达到最大值时,以26万元卖出,问哪一种方案较为合算?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】挑选空间飞行员可以说是“万里挑一”,要想通过需要五关:目测、初检、复检、文考(文化考试)、政审.若某校甲、乙、丙三位同学都顺利通过了前两关,根据分析甲、乙、丙三位同学通过复检关的概率分别是0.5、0.6、0.75,能通过文考关的概率分别是0.6、0.5、0.4,由于他们平时表现较好,都能通过政审关,若后三关之间通过与否没有影响.
(1)求甲被录取成为空军飞行员的概率;
(2)求甲、乙、丙三位同学中恰好有一个人通过复检的概率;
(3)设只要通过后三关就可以被录取,求录取人数![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着城市地铁建设的持续推进,市民的出行也越来越便利.根据大数据统计,某条地铁线路运行时,发车时间间隔t(单位:分钟)满足:![]() ,平均每趟地铁的载客人数
,平均每趟地铁的载客人数![]() (单位:人)与发车时间间隔
(单位:人)与发车时间间隔![]() 近似地满足下列函数关系:
近似地满足下列函数关系: ,其中
,其中![]() .
.
(1)若平均每趟地铁的载客人数不超过1000人,试求发车时间间隔t的值;
(2)若平均每趟地铁每分钟的净收益为![]()
![]() (单位:元),问当发车时间间隔t为多少分钟时,平均每趟地铁每分钟的净收益最大? 并求出最大净收益.
(单位:元),问当发车时间间隔t为多少分钟时,平均每趟地铁每分钟的净收益最大? 并求出最大净收益.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com