练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图ABCD﹣A1B1C1D1是长方体，O是B1D1的中点，直线AC1交平面CB1D1于点M，则下列结论正确的是（ ）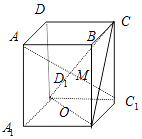

    A.C，M，O三点共线
    B.C，M，O，A1不共面
    C.A，M，O，C不共面
    D.B，M，O，B1共面

    【答案】A
    【解析】解：连接A1C1 ， AC，则A1C1∥AC，
    ∴A1、C1、C、A四点共面，
    ∴A1C平面ACC1A1 ，
    ∵M∈A1C，∴M∈平面ACC1A1 ， 又M∈平面CB1D1 ，
    ∴M在平面ACC1A1与平面CB1D1的交线上，
    同理O在平面ACC1A1与平面CB1D1的交线上，
    ∴C、M、O三点共线．
    故选：A．
    【考点精析】解答此题的关键在于理解棱柱的结构特征的相关知识，掌握两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】近几年，电商行业的蓬勃发展也带动了快递业的高速发展.某快递配送站每天至少要完成1800件包裹的配送任务，该配送站有8名新手快递员和4名老快递员，但每天最多安排10人进行配送.已知每个新手快递员每天可配送240件包裹，日工资320元；每个老快递员每天可配送300件包裹，日工资520元.

    (Ⅰ)求该配送站每天需支付快递员的总工资最小值；

    (Ⅱ)该配送站规定:新手快递员某个月被评为“优秀”，则其下个月的日工资比这个月提高12%.那么新手快递员至少连续几个月被评为“优秀”，日工资会超过老快递员?

    (参考数据: ， ， .)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆E： 的左、右焦点分别为F1、F2 ， 离心率 ，P为椭圆E上的任意一点（不含长轴端点），且△PF1F2面积的最大值为1．
    （1）求椭圆E的方程；
    （2）已知直x﹣y+m=0与椭圆E交于不同的两点A，B，且线AB的中点不在圆 内，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C：x2+y2﹣2x﹣2ay+a2﹣24=0（a∈R）的圆心在直线2x﹣y=0上．
    （1）求实数a的值；
    （2）求圆C与直线l：（2m+1）x+（m+1）y﹣7m﹣4=0（m∈R）相交弦长的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=4sinθ．
    （1）求曲线C的直角坐标方程；
    （2）若曲线C1： （α为参数）与曲线C所表示的图形都相切，求r的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义域为R的函数f（x）= 满足f（0）=0．
    （1）求a，f（﹣2）的值，判断函数f（x）的奇偶性并说明理由；
    （2）判断该函数在R上的单调性（不要求证明），解不等式f（x2+x）＜ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于x的不等式ax2﹣|x+1|+3a≥0的解集为（﹣∞，+∞），则实数a的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，定义在[﹣1，5]上的函数f（x）由一段线段和抛物线的一部分组成． （Ⅰ）求函数f（x）的解析式；
    （Ⅱ）指出函数f（x）的自变量x在什么范围内取值时，函数值大于0，小于0或等于0（不需说理由）．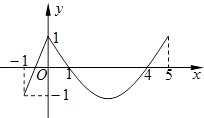

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知| |=4，| |=2，且 与 夹角为120°求：
    （1）（ ﹣2 ）（ + ）；
    （2） 在 上的投影；
    （3） 与 + 的夹角．

    查看答案和解析>>

    同步练习册答案