
【题目】如图,在边长为2菱形ABCD中,![]() ,且对角线AC与BD交点为O.沿BD将
,且对角线AC与BD交点为O.沿BD将![]() 折起,使点A到达点
折起,使点A到达点![]() 的位置.
的位置.

(1)若![]() ,求证:
,求证:![]() 平面ABCD;
平面ABCD;
(2)若![]() ,求三棱锥
,求三棱锥![]() 体积.
体积.
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
【题目】现有甲、乙、丙三个盒子,其中每个盒子中都装有标号分别为1、2、3、4、5、6的六张卡片,现从甲、乙、丙三个盒子中依次各取一张卡片使得卡片上的标号恰好成等差数列的取法数为( )
A.14B.16C.18D.20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种产品,每日的成本C(单位:万元)与日产量x(单位:吨)满足函数关系式C=4+x,每日的销售额S(单位:万元)与日产量x满足函数关系式
S=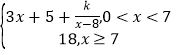 ,已知每日的利润L=S﹣C,且当x=4时,L=7.
,已知每日的利润L=S﹣C,且当x=4时,L=7.
(1)求k;
(2)当日产量为多少吨时,每日的利润可以达到最大?并求此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理是合情推理的是( )
①由圆的性质类比出球的有关性质;
②由直角三角形、等腰三角形、等边三角形内角和是![]() 归纳出所有三角形的内角和都是
归纳出所有三角形的内角和都是![]()
③由![]() ,满足
,满足![]() ,推出
,推出![]() 是奇函数;
是奇函数;
④三角形内角和是![]() ,四边形内角和是
,四边形内角和是![]() ,五边形内角和是
,五边形内角和是![]() ,由此得凸多边形内角和是
,由此得凸多边形内角和是![]() .
.
A. ①②④B. ①③④C. ②④D. ①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市在开展创建“全国文明城市”活动中,工作有序扎实,成效显著,尤其是城市环境卫生大为改观,深得市民好评.“创文”过程中,某网站推出了关于环境治理和保护问题情况的问卷调查,现从参与问卷调查的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
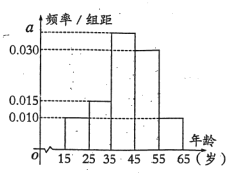
(1)求出a的值;
(2)若已从年龄较小的第1,2组中用分层抽样的方法抽取5人,现要再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正整数数列中,由1开始依次按如下规则,将某些整数染成红色,先染1;再染3个偶数2,4,6;再染6后面最邻近的5个连续奇数7,9,11,13,15;再染15后面最邻近的7个连续偶数16,18,20,22,24,26,28;再染此后最邻近的9个连续奇数29,31,…,45;按此规则一直染下去,得到一红色子数列:1,2,4,6,7,9,11,13,15,16,……,则在这个红色子数列中,由1开始的第2019个数是( )
A. 3972 B. 3974 C. 3991 D. 3993
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com