
| A. | 1 | B. | $\frac{7}{8}$ | C. | $\frac{9}{8}$ | D. | 2 |
分析 由已知可得$\frac{a}{3}+\frac{b}{3}=1$,代入$\frac{1}{1+a}+\frac{4}{4+b}$,然后利用基本不等式求最值.
解答 解:∵a+b=3,
∴$\frac{1}{1+a}+\frac{4}{4+b}$=$\frac{\frac{a}{3}+\frac{b}{3}}{1+a}+\frac{\frac{4a}{3}+\frac{4b}{3}}{4+b}$=$\frac{\frac{a}{3}+\frac{b}{3}}{\frac{4a}{3}+\frac{b}{3}}+\frac{\frac{4a}{3}+\frac{4b}{3}}{\frac{4a}{3}+\frac{7b}{3}}$
=$\frac{\frac{1}{8}(\frac{4a}{3}+\frac{b}{3})+\frac{1}{8}(\frac{4a}{3}+\frac{7b}{3})}{\frac{4a}{3}+\frac{b}{3}}+\frac{\frac{1}{2}(\frac{4a}{3}+\frac{b}{3})+\frac{1}{2}(\frac{4a}{3}+\frac{7b}{3})}{\frac{4a}{3}+\frac{7b}{3}}$
=$\frac{1}{8}+\frac{1}{2}+\frac{\frac{1}{8}(\frac{4a}{3}+\frac{7b}{3})}{\frac{4a}{3}+\frac{b}{3}}+\frac{\frac{1}{2}(\frac{4a}{3}+\frac{b}{3})}{\frac{4a}{3}+\frac{7b}{3}}$$≥\frac{5}{8}+2\sqrt{\frac{1}{8}×\frac{1}{2}}=\frac{5}{8}+\frac{1}{2}=\frac{9}{8}$.
当且仅当$(\frac{4a}{3}+\frac{7b}{3})=2(\frac{4a}{3}+\frac{b}{3})$,即a=$\frac{5}{3}$,b=$\frac{4}{3}$时等号成立.
故选:C.
点评 本题考查利用基本不等式求最值,关键是掌握该类问题的求解方法,是中档题.


 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{10}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $-\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{\sqrt{10}}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
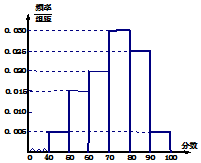 某校从高三年级期末考试的学生中抽出20名学生,其成绩(均为整数)的频率分布直方图如图所示:
某校从高三年级期末考试的学生中抽出20名学生,其成绩(均为整数)的频率分布直方图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果m?α,n?α,m、n是不在任何同一个平面内的直线,那么n∥α | |
| B. | 如果m?α,n?α,m、n是不在任何同一个平面内的直线,那么n与α相交 | |
| C. | 如果m∥α,n∥α,m、n共面,那么m∥n | |
| D. | 如果m?α,n∥α,m、n共面,那么m∥n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com