
【题目】在平面直角坐标系中,直线L的参数方程为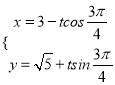 (
(![]() 为参数).在以原点
为参数).在以原点 ![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标中,圆C的方程为
轴正半轴为极轴的极坐标中,圆C的方程为![]() .
.
(Ⅰ)写出直线L的倾斜角![]() 和圆C的直角坐标方程;
和圆C的直角坐标方程;
(Ⅱ)若点 P坐标为![]() ,圆C与直线L交于 A,B两点,求|PA|
,圆C与直线L交于 A,B两点,求|PA|![]() |PB|的值.
|PB|的值.
的值.
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】已知圆C的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() .若直线
.若直线![]() 与圆C相交于不同的两点P,Q.
与圆C相交于不同的两点P,Q.
(Ⅰ)写出圆C的直角坐标方程,并求圆心的坐标与半径;
(Ⅱ)若弦长|PQ|=4,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个正数a,b,可按规则![]() 扩充为一个新数c,在a,b,c三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
扩充为一个新数c,在a,b,c三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
(1)若a=1,b=3,按上述规则操作三次,扩充所得的数是_____________;
(2)若p>q>0,经过6次操作后扩充所得的数为![]() (m,n为正整数),
(m,n为正整数),
则m,n的值分别为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两支篮球队进行一局比赛,甲获胜的概率为0.6,若采用三局两胜制举行一次比赛,现采用随机模拟的方法估计乙获胜的概率.
先利用计算器或计算机生成0到9之间取整数值的随机数,用0,1,2,3,4,5表示甲获胜;6,7,8,9表示乙获胜,这样能体现甲获胜的概率为0.6.因为采用三局两胜制,所以每3个随机数作为一组.例如,产生30组随机数.
034 743 738 636 964 736 614 698 637 162 332 616 804 560 111 410 959 774 246 762 428 114 572 042 533 237 322 707 360 751
据此估计乙获胜的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果对任意的
,如果对任意的![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 为
为![]() 阶伸缩函数.
阶伸缩函数.
(![]() )若函数
)若函数![]() 为二阶伸缩函数,且当
为二阶伸缩函数,且当![]() 时,
时, ![]() ,求
,求![]() 的值.
的值.
(![]() )若
)若![]() 为三阶伸缩函数,且当
为三阶伸缩函数,且当![]() 时,
时, ![]() ,求证:函数
,求证:函数![]() 在
在![]() 上无零点.
上无零点.
(![]() )若函数
)若函数![]() 为
为![]() 阶伸缩函数,且当
阶伸缩函数,且当![]() 时,
时, ![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 在
在![]() 上的取值范围.
上的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大西洋鲑鱼每年都要逆流而上,游回产地产卵.记鲑鱼的游速为![]() ,鲑鱼的耗氧量的单位数为
,鲑鱼的耗氧量的单位数为![]() ,研究中发现
,研究中发现![]() 与
与![]() 成正比,且当
成正比,且当![]() 时,
时, ![]() .
.
(1)求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)计算一条鲑鱼的游速是![]() 时耗氧量的单位数;
时耗氧量的单位数;
(3)当鲑鱼的游速增加![]() 时,其耗氧量是原来的几倍?
时,其耗氧量是原来的几倍?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com