
| A. | (2,+∞) | B. | [2,+∞) | C. | (4,+∞) | D. | [4,+∞) |
分析 x+y=1代入$\frac{1}{x}+\frac{1}{y}$,然后根据基本不等式即可求出$\frac{1}{x}+\frac{1}{y}$的范围,从而找出正确选项.
解答 解:x,y>0,且x+y=1;
∴$\frac{1}{x}+\frac{1}{y}=\frac{x+y}{x}+\frac{x+y}{y}$
=$1+\frac{y}{x}+\frac{x}{y}+1$
=$2+\frac{y}{x}+\frac{x}{y}$
≥2+2;
当$\frac{y}{x}=\frac{x}{y}$,即x=y时取“=”;
∴$\frac{1}{x}+\frac{1}{y}$的取值范围为[4,+∞).
故选D.
点评 考查基本不等式的应用,并判断等号能否取到.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 在区间(-1,0)内没有实数根 | |
| B. | 在区间(-1,0)内有一个实数根,在(-1,0)外有一个实数根 | |
| C. | 在区间(-1,0)内有两个相等的实数根 | |
| D. | 在区间(-1,0)内有两个不相等的实数根 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高二文下学期期末考试数学试卷(解析版) 题型:选择题
已知函数 满足对任意的实数
满足对任意的实数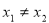 都有
都有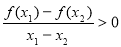 ,则a的取值范围是( )
,则a的取值范围是( )
A.﹣3≤a<0 B.﹣3≤a≤﹣2 C.a≤﹣2 D.a<0
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60 | B. | 66 | C. | 72 | D. | 78 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com