
【题目】关于平面向量,有下列四个命题:
①若 ![]() .
.
② ![]() =(1,1),
=(1,1), ![]() =(2,x),若
=(2,x),若 ![]() 与
与 ![]() 平行,则x=2.
平行,则x=2.
③非零向量 ![]() 和
和 ![]() 满足|
满足| ![]() |=|
|=| ![]() |=|
|=| ![]() |,则
|,则 ![]() 与
与 ![]() 的夹角为60°.
的夹角为60°.
④点A(1,3),B(4,﹣1),与向量 ![]() 同方向的单位向量为(
同方向的单位向量为( ![]() ).
).
其中真命题的序号为 . (写出所有真命题的序号)
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】在公务员招聘中,既有笔试又有面试,某单位在2015年公务员考试中随机抽取100名考生的笔试成绩,按成绩分为5组[50,60),[60,70),[70,80),[80,90),[90,100],得到的频率分布直方图如图所示. 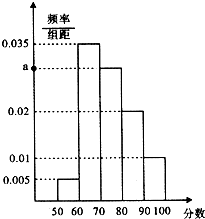
(1)求a值及这100名考生的平均成绩;
(2)若该单位决定在成绩较高的第三、四、五组中按分层抽样抽取6名考生进入第二轮面试,现从这6名考生中抽取3名考生接受单位领导面试,设第四组中恰有1名考生接受领导面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD中, 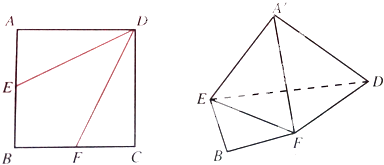
(1)点E是AB的中点,点F是BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.求证:A′D⊥EF
(2)当BE=BF= ![]() BC时,求三棱锥A′﹣EFD的体积.
BC时,求三棱锥A′﹣EFD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数F(x)= ![]() ,其中f(x)=log2(x2+1),g(x)=log2(|x|+7).
,其中f(x)=log2(x2+1),g(x)=log2(|x|+7).
(1)在实数集R上用分段函数形式写出函数F(x)的解析式;
(2)求函数F(x)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,B1CAC1
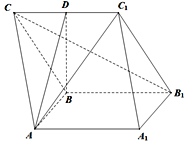
(Ⅰ)求证:平面AA1B1B面BB1C1C;
(Ⅱ)若D是CC1中点,ADB是二面角A-CC1-B的平面角,求直线AC1与平面ABC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以原点为圆心,椭圆的短半轴为半径的圆与直线x﹣y+
,以原点为圆心,椭圆的短半轴为半径的圆与直线x﹣y+ ![]() =0相切,过点P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点.
=0相切,过点P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点.
(1)求椭圆C的方程;
(2)求 ![]() 的取值范围;
的取值范围;
(3)若B点关于x轴的对称点是E,证明:直线AE与x轴相交于定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(1)+f(2)+f(3)+…+f(2013)+f(2014)+f(2015)+f(2016)的值分别为( ) 
A.f(x)= ![]() sin
sin ![]() x+1,S=2016
x+1,S=2016
B.f(x)= ![]() cos
cos ![]() x+1,S=2016
x+1,S=2016
C.f(x)= ![]() sin
sin ![]() x+1,S=2016.5
x+1,S=2016.5
D.f(x)= ![]() cos
cos ![]() x+1,S=2016.5
x+1,S=2016.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com