
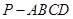 为正四棱锥,几何体
为正四棱锥,几何体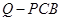 为正四面体.、
为正四面体.、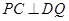 ;
;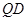 与平面
与平面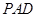 所成角的正弦值.
所成角的正弦值.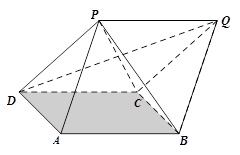
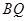 的中点
的中点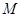 ,连结
,连结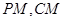 ,由几何体
,由几何体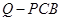 为正四面体得,
为正四面体得,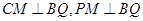 ,所以
,所以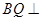 平面
平面 ,从而
,从而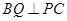 .
.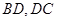 交于点
交于点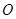 ,连结
,连结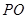 得
得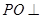 平面
平面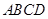 ,
, ,所以
,所以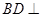 平面
平面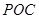 ,从而
,从而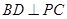 .又
.又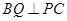
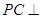 平面
平面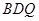 ,从而
,从而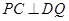 .
.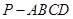 为正四棱锥,几何体
为正四棱锥,几何体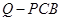 为正四面体.
为正四面体.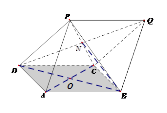
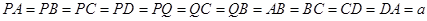
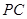 的中点
的中点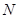 ,连结
,连结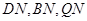 ,由题意知
,由题意知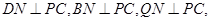
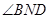 是二面角
是二面角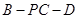 的平面角,
的平面角, 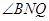 是二面角
是二面角 的平面角,
的平面角,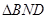 中,
中,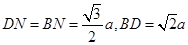 ,
,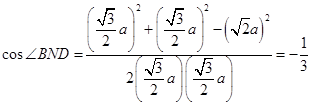 ,
,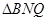 中,
中,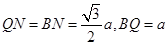 ,
,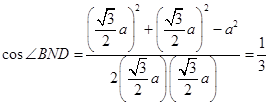
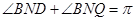 ,从而
,从而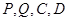 四点共面,
四点共面,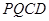 为菱形,从而
为菱形,从而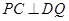
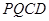 为菱形,于是
为菱形,于是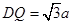 ,
,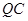 ∥
∥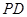 ,
,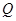 到平面
到平面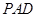 的距离等于点
的距离等于点 到平面
到平面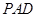 的距离,
的距离, 到平面
到平面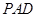 的距离为
的距离为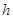 ,由
,由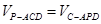 得:
得: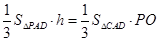
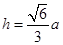 ,所以
,所以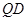 与平面
与平面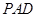 所成角的正弦值
所成角的正弦值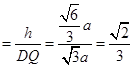
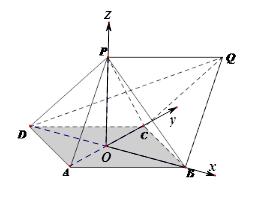
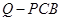 为正四面体,所以
为正四面体,所以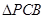 为正三角形,所以
为正三角形,所以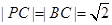 ,所以
,所以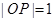 ,因此P(0,0,1)。
,因此P(0,0,1)。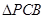 的重心为M,则
的重心为M,则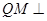 面PCB,又
面PCB,又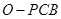 也为正三棱锥,因此
也为正三棱锥,因此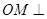 面PCB,因此O、M、Q三点共线,所以OQ垂直面PCB,即
面PCB,因此O、M、Q三点共线,所以OQ垂直面PCB,即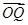 是平面PCB的一个法向量,
是平面PCB的一个法向量,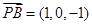 ,
,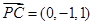 易得平面PCB的一个法向量可以取
易得平面PCB的一个法向量可以取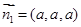 ,所以不妨设Q(a,a,a),则
,所以不妨设Q(a,a,a),则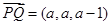 ,因为
,因为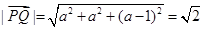 解得a=1,所以Q(1,1,1)。
解得a=1,所以Q(1,1,1)。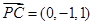 ,
,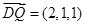 ,
,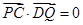 ,所以
,所以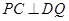 ;
;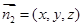 ,
,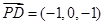 ,
,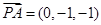 ,由
,由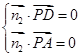 解得一个法向量
解得一个法向量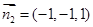 ,
,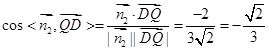 ,所以QD与平面PAD所成角的正弦值为
,所以QD与平面PAD所成角的正弦值为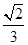 。
。

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
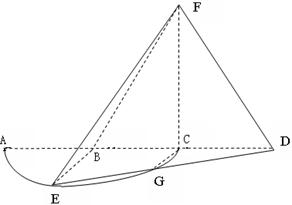
 是半径为
是半径为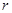 的半圆,
的半圆,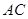 为直径,点
为直径,点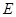 为弧
为弧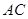 的中点,点
的中点,点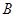 和点
和点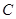 为线段
为线段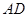 的三等分点,线段
的三等分点,线段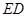 与弧
与弧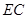 交于点
交于点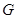 ,且
,且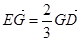 ,平面
,平面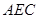 外一点
外一点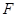 满足
满足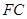
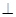 平面
平面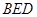 ,
,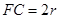 。
。
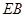
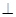
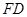 ;
; (及其内部)绕
(及其内部)绕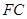 所在直线旋转一周形成一几何体,求该几何体的体积。
所在直线旋转一周形成一几何体,求该几何体的体积。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.一条直线和一个平面平行,它就和这个平面内的任一条直线平行 |
| B.平行于同一平面的两条直线平行 |
| C.如果一个平面内的无数条直线平行于另一个平面,则这两个平面平行 |
| D.如果一个平面内任何一条直线都平行于另一个平面,则这两个平面平行 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
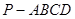 中,AB=1,侧棱
中,AB=1,侧棱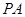 与底面
与底面 所成角的正切值为
所成角的正切值为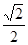 .
.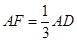 ,求点A到平面PB
,求点A到平面PB F的距离.
F的距离.
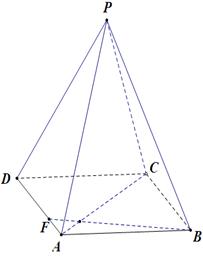
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com