
【题目】已知函数f(x)对任意实数x,y均有f(x)=f( ![]() )+f(
)+f( ![]() ).当x>0时,f(x)>0
).当x>0时,f(x)>0
(1)判断函数f(x)在R上的单调性并证明;
(2)设函数g(x)与函数f(x)的奇偶性相同,当x≥0时,g(x)=|x﹣m|﹣m(m>0),若对任意x∈R,不等式g(x﹣1)≤g(x)恒成立,求实数m的取值范围.
【答案】
(1)解:由题意:函数f(x)对任意实数x,y均有f(x)=f( ![]() )+f(
)+f( ![]() ),令x=y=0,可得f(0)=0.设x1>x2,令x=x1,y=x2,
),令x=y=0,可得f(0)=0.设x1>x2,令x=x1,y=x2,
则 ![]() ,
,
可得:则 ![]() ,即
,即 ![]() >0.
>0.
∴函数f(x)在R上是单调增函数.
(2)解:令x=0,y=2x,
可得:f(0)=0=f(x)+f(﹣x),即f(﹣x)=﹣f(x).
∴f(x)是奇函数,故得g(x)也是奇函数.
当x≥0时,g(x)=|x﹣m|﹣m(m>0),
即g(x)= 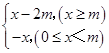
当x<0时,g(x)的最大值为m.
对任意x∈R,不等式g(x﹣1)≤g(x)恒成立,
只需要:1≥3m﹣(﹣2m),
解得: ![]() .
.
∵m>0
故得实数m的取值范围是(0, ![]() ].
].
【解析】(1)函数f(x)对任意实数x,y均有f(x)=f( ![]() )+f(
)+f( ![]() ),令x=y=0,可得f(0)=0.设x1>x2,令x=x1,y=x2,带入f(x)=f(
),令x=y=0,可得f(0)=0.设x1>x2,令x=x1,y=x2,带入f(x)=f( ![]() )+f(
)+f( ![]() ).利用x>0时,f(x)>0,可判断单调性.(2)求解f(x)的奇偶性,可得g(x)的奇偶性,x≥0时,g(x)=|x﹣m|﹣m(m>0),利用奇偶性求g(x)的解析式,判断单调性,从而求解不等式g(x﹣1)≤g(x)恒成立时实数m的取值范围.
).利用x>0时,f(x)>0,可判断单调性.(2)求解f(x)的奇偶性,可得g(x)的奇偶性,x≥0时,g(x)=|x﹣m|﹣m(m>0),利用奇偶性求g(x)的解析式,判断单调性,从而求解不等式g(x﹣1)≤g(x)恒成立时实数m的取值范围.
【考点精析】关于本题考查的函数的奇偶性,需要了解偶函数的图象关于y轴对称;奇函数的图象关于原点对称才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】某营养师要求为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营状中至少含64个单位的碳水化合物和42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+(y﹣1)2=9,直线l:x﹣my+m﹣2=0,且直线l与圆C相交于A、B两点. (Ⅰ)若|AB|=4 ![]() ,求直线l的倾斜角;
,求直线l的倾斜角;
(Ⅱ)若点P(2,1)满足 ![]() =
= ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面为正方形的四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,PA⊥AD,PA=AD,则异面直线PB与AC所成的角为( ) 
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,c= ![]() asinC﹣ccosA.
asinC﹣ccosA.
(1)求A;
(2)若a=2,△ABC的面积为 ![]() ,求b,c.
,求b,c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|2a﹣x|+2x,a∈R.
(1)若a=0,判断函数y=f(x)的奇偶性,并加以证明;
(2)若函数f(x)在R上是增函数,求实数a的取值范围;
(3)若存在实数a∈[﹣2,2],使得关于x的方程f(x)﹣tf(2a)=0有三个不相等的实数根,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,M,E,F,N分别为A1B1 , B1C1 , C1D1 , D1A1的中点,求证: 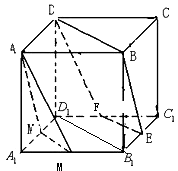
(1)E,F,D,B四点共面;
(2)面AMN∥平面EFDB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)满足对任意的两个不相等的正数x1 , x2 , 下列三个式子:f(x1﹣x2)+f(x2﹣x1)=0,(x1﹣x2)(f(x1)﹣f(x2))<0,f( ![]() )>
)> ![]() 都恒成立,则f(x)可能是( )
都恒成立,则f(x)可能是( )
A.f(x)= ![]()
B.f(x)=﹣x2
C.f(x)=﹣tanx
D.f(x)=|sinx|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com