已知函数f(x)=ex-1-e1-x.
(1)该函数图象上是否存在不同两点A、B,使过A、B的直线平行于x轴?证明你的结论;
(2)若函数h(x)=f(25-|x+1|-4•5-|x+1|-m+1)存在零点,求实数m的取值范围.
解:(1)函数图象上不存在不同两点A、B,使过A、B的直线平行于x轴,证明如下:
由函数f(x)=e
x-1-e
1-x知,此函数中e
x-1是一个增函数,e
1-x是一个减函数,故f(x)=e
x-1-e
1-x是一个增函数,
由此知函数图象上不可能存在两个不同的点,其纵坐标相等,即该函数图象上不存在不同两点A、B,使过A、B的直线平行于x轴
(2)由(1)知,函数f(x)=e
x-1-e
1-x是一个增函数,当f(x)=0时必有e
x-1=e
1-x 成立,即有x-1=1-x,即x=1时函数值为0
又函数h(x)=f(25
-|x+1|-4•5
-|x+1|-m+1)存在零点,故25
-|x+1|-4•5
-|x+1|-m+1=1,整理得m=25
-|x+1|-4•5
-|x+1|,
不妨令t=5
-|x+1|=
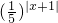
,所以t∈(0,1)
即m=t
2-4t=(m-2)
2-4,t∈(0,1),
∴m∈(-3,0)
分析:(1)观察知,此函数是一个增函数,故不存在不同两点A、B,使过A、B的直线平行于x轴,证明出函数是一个增函数,即可说明结论;
(2)由(1)知,f(x)=0时必有e
x-1=e
1-x 成立,解得x=1,由此知函数h(x)=f(25
-|x+1|-4•5
-|x+1|-m+1)存在零点必有25
-|x+1|-4•5
-|x+1|-m+1=1从而得到m=25
-|x+1|-4•5
-|x+1|,利用换元法,将其转化为二次函数,解出值域即得实数m的取值范围.
点评:本题考查函数与方程的综合运用,考查了指数型函数单调性的判断,函数恒存在零点的问题,解题的关键是理解题意,将所研究的问题准确转化,第一小题中转化为研究函数图象上有没有两点纵坐标相等,第二小题中由函数一定存在零点转化出m的方程,将方程转化为函数,从而借助求函数的值域求出实数m的取值范围,本题综合性强,是能力型题,由题设条件分析出解决问题的方法是本题的重点.

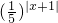 ,所以t∈(0,1)
,所以t∈(0,1)

 考前必练系列答案
考前必练系列答案