
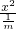 +
+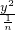 =1,由“mn<0”,可得
=1,由“mn<0”,可得 、
、 异号,可得方程表示双曲线,由此可得“mn<0”是方程“mx2+ny2=1表示双曲线”的充分条件;再证必要性,先把方程化为
异号,可得方程表示双曲线,由此可得“mn<0”是方程“mx2+ny2=1表示双曲线”的充分条件;再证必要性,先把方程化为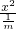 +
+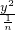 =1,由双曲线方程的形式可得
=1,由双曲线方程的形式可得 、
、 异号,进而可得mn<0,由此可得“mn<0”是方程“mx2+ny2=1表示双曲线”的必要条件;综合可得答案.
异号,进而可得mn<0,由此可得“mn<0”是方程“mx2+ny2=1表示双曲线”的必要条件;综合可得答案.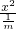 +
+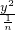 =1,
=1, 、
、 异号,方程
异号,方程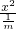 +
+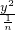 =1中,两个分母异号,则其表示双曲线,
=1中,两个分母异号,则其表示双曲线,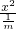 +
+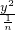 =1,
=1, 、
、 异号,则必有mn<0,
异号,则必有mn<0,

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com