
【题目】已知有穷数列![]() 共有
共有![]() 项
项![]() ,首项
,首项![]() ,设该数列的前
,设该数列的前![]() 项和为
项和为![]() ,且
,且![]()
![]() 其中常数
其中常数![]() .
.
(1)求证:数列![]() 是等比数列
是等比数列
(2)若![]() ,数列
,数列![]() 满足
满足![]()
![]() ,求出数列
,求出数列![]() 的通项公式
的通项公式
(3)若(2)中的数列![]() 满足不等式
满足不等式![]() ,求出
,求出![]() 的值
的值
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() ,满足
,满足![]() .
.
(1)若![]() ,求数列前10项和;
,求数列前10项和;
(2)若![]() ,且数列
,且数列![]() 前2017项中有100项是0,求
前2017项中有100项是0,求![]() 的可能值;
的可能值;
(3)求证:在数列![]() 中,存在
中,存在![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的4月23日为“世界读书日”,某调查机构对某校学生做了一个是否喜爱阅读的抽样调查.该调查机构从该校随机抽查了100名不同性别的学生(其中男生45名),统计了每个学生一个月的阅读时间,其阅读时间![]() (小时)的频率分布直方图如图所示:
(小时)的频率分布直方图如图所示:
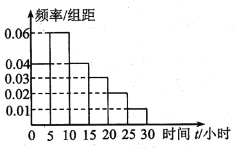
(1)求样本学生一个月阅读时间![]() 的中位数
的中位数![]() .
.
(2)已知样本中阅读时间低于![]() 的女生有30名,请根据题目信息完成下面的
的女生有30名,请根据题目信息完成下面的![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下认为阅读与性别有关.
列联表,并判断能否在犯错误的概率不超过0.1的前提下认为阅读与性别有关.
![]() 列联表
列联表
男 | 女 | 总计 | |
| |||
| |||
总计 |
附表:
| 0.15 | 0.10 | 0.05 |
| 2.072 | 2.706 | 3.841 |
其中: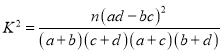 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|3x+2|.
(1)解不等式f(x)<4-|x-1|;
(2)已知m+n=1(m,n>0),若|x-a|-f(x)≤![]() (a>0)恒成立,求实数a的取值范围.
(a>0)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示为一名曰“堑堵”的几何体,已知 AE⊥底面BCFE , DF ∥ AE , DF = AE = 1, CE =![]() ,四边形ABCD 是正方形.
,四边形ABCD 是正方形.
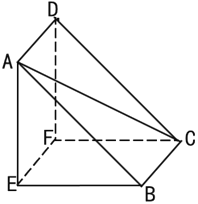
(1)《九章算术》中将四个面都是直角三角形的四面体称为鳖臑.判断四面体 EABC 是否为鳖臑,若是,写出其 每一个面的直角,并证明;若不是,请说明理由.
(2)求四面体 EABC 的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com