解:(1)f′(x)=3x
2+2ax-2
∵f(x)=x
3+ax
2-2x+5在(

,1)上递减,在(1,+∞)上递增,
∴f′(1)=0,
∴a=-

. …(6分)
(2)令f′(x)=3x
2+2ax-2=0.
∵△=4a
2+24>0,∴方程有两个实根,…(8分)
分别记为x
1 x
2.由于x
1•x
2=-

,说明x
1,x
2一正一负,
即在(

,1)内方程f′(x)=0不可能有两个解.…(10分)
故要使得f(x)在(

,

)上既不是单调增函数也不是单调减函数的充要条件是
f′(

)•f′(

)<0,即(

+

a-2)(

+a-2)<0.…(13分)
解得
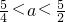
. …(15分)
∵a是正整数,∴a=2.…(16分)
分析:(1)先求导函数,再根据f(x)=x
3+ax
2-2x+5在(

,1)上递减,在(1,+∞)上递增,可得f′(1)=0,从而可求实数a的值;
(2)求出函数的导数,由题意得在(

,1)内方程f′(x)=0不可能有两个解,故要使得f(x)在(

,

)上既不是单调增函数也不是单调减函数的充要条件是f′(

)•f′(

)<0,从而可得实数a的取值范围.
点评:本题以函数为载体,考查函数的单调性,考查函数的极值,同时考查学生分析解决问题的能力,解题的关键是得出在(

,1)内方程f′(x)=0不可能有两个解

 ,1)上单调递减,在(1,+∞)上单调递增,求实数a的值;
,1)上单调递减,在(1,+∞)上单调递增,求实数a的值; ,
, )上既不是单调递增函数也不是单调递减函数?若存在,试求出a的值,若不存在,请说明理由.
)上既不是单调递增函数也不是单调递减函数?若存在,试求出a的值,若不存在,请说明理由. ,1)上递减,在(1,+∞)上递增,
,1)上递减,在(1,+∞)上递增, . …(6分)
. …(6分) ,说明x1,x2一正一负,
,说明x1,x2一正一负, ,1)内方程f′(x)=0不可能有两个解.…(10分)
,1)内方程f′(x)=0不可能有两个解.…(10分) ,
, )上既不是单调增函数也不是单调减函数的充要条件是
)上既不是单调增函数也不是单调减函数的充要条件是 )•f′(
)•f′( )<0,即(
)<0,即( +
+ a-2)(
a-2)( +a-2)<0.…(13分)
+a-2)<0.…(13分)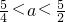 . …(15分)
. …(15分) ,1)上递减,在(1,+∞)上递增,可得f′(1)=0,从而可求实数a的值;
,1)上递减,在(1,+∞)上递增,可得f′(1)=0,从而可求实数a的值; ,1)内方程f′(x)=0不可能有两个解,故要使得f(x)在(
,1)内方程f′(x)=0不可能有两个解,故要使得f(x)在( ,
, )上既不是单调增函数也不是单调减函数的充要条件是f′(
)上既不是单调增函数也不是单调减函数的充要条件是f′( )•f′(
)•f′( )<0,从而可得实数a的取值范围.
)<0,从而可得实数a的取值范围. ,1)内方程f′(x)=0不可能有两个解
,1)内方程f′(x)=0不可能有两个解 

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<