
判定下列命题的真、假:
(1)
垂直于同一条直线的两直线平行;(2)
垂直于同一个平面的两直线平行;(3)
一条直线与一个平面内的一条直线不垂直,那么这条直线就一定不与这个平面垂直;(4)
一条直线和一个平面都垂直于同一条直线,则这条直线和平面平行;(5)a
、b、c为三条直线,若a⊥b,b⊥c,则a⊥c;(6)
过已知点作已知平面的垂线,和过已知点作已知直线的垂线,都是有且只有一条;(7)
如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直;(8)
垂直于三角形两边的直线必垂直于第三边.|
从直线与平面的位置关系、直线与平面的垂直定义入手,逐一判断真伪. 解: (1)垂直于同一条直线的两条直线可能平行,也可能相交或异面.如图所示,正方体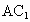 中,AB与 中,AB与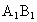 都与 都与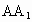 垂直,此时AB∥ 垂直,此时AB∥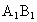 ;AD与AB都与 ;AD与AB都与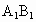 垂直,此时AD∩AB=A;AB与 垂直,此时AD∩AB=A;AB与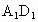 都与 都与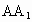 垂直,此时AB与 垂直,此时AB与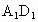 异面.故该命题为假命题; 异面.故该命题为假命题;
(2)该命题的结论为课本定理,故是真命题; (3)如果一条直线垂直于一个平面,那么这条直线垂直于这个平面内的任何一条直线.一条直线和平面内的一条直线不垂直,则不具备线面垂直定义的要求.故是真命题; (4)若直线在平面内,则满足命题的条件:一条直线和一个平面都垂直于同一条直线.故是假命题; (5)同(1)中图可知,a与c位置关系可以平行.故是假命题; (6)由唯一性结论知,过已知点作已知平面的垂线只有一条是正确的;而过已知点作已知直线的垂线则有无数多条,如图中,过点A作直线与 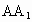 垂直,由于 垂直,由于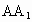 ⊥平面ABCD,可知平面ABCD内的所有直线都与 ⊥平面ABCD,可知平面ABCD内的所有直线都与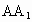 垂直.故是假命题; 垂直.故是假命题;
(7)该命题的关键是这无数条直线具有怎样的位置关系.①若为平行,则该命题应打“×”号;若为相交,则该命题应打“√”.正是因为这两种情况可能同时具备,因此,不说明面内这个无数条线的位置关系.故是假命题; (8)由直线与平面垂直的判定定理知,垂直于三角形两边的直角必垂直于这个三角形所在的平面,从而也必垂直于其第三边.故它为真命题. 本题是利用直线和平面垂直的定义及判定定理等知识:来解答的问题。解答此类问题必须做到:概念清楚,问题理解透彻,相关知识能灵活运用. |


科目:高中数学 来源:数学教研室 题型:022
判定下列命题的真、假:
(1)垂直于同一条直线的两直线平行;
(2)垂直于同一个平面的两直线平行;
(3)一条直线与一个平面内的一条直线不垂直,那么这条直线就一定不与这个平面垂直;
(4)一条直线和一个平面都垂直于同一条直线,则这条直线和平面平行;
(5)a、b、c为三条直线,若a⊥b,b⊥c,则a⊥c;
(6)过已知点作已知平面的垂线,和过已知点作已知直线的垂线,都是有且只有一条;
(7)如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直;
(8)垂直于三角形两边的直线必垂直于第三边.
查看答案和解析>>
科目:高中数学 来源:2013届安徽省高二下学期期中考试文科数学试卷(解析版) 题型:解答题
命题p:关于 的不等式
的不等式 的解集为
的解集为 ;
;
命题q:函数 为增函数.
为增函数.
分别求出符合下列条件的实数 的取值范围.
的取值范围.
(1)p、q至少有一个是真命题;(2)p∨q是真命题且p∧q是假命题.
【解析】本试题主要考查了函数的单调性,不等式的解集,以及命题的真值判定的综合运用。
查看答案和解析>>
科目:高中数学 来源:新课标高三数学抛物线、直线与圆锥曲线的位置关系专项训练(河北) 题型:解答题
命题p:关于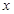 的不等式
的不等式 的解集为
的解集为 ;
;
命题q:函数 为增函数.
为增函数.
分别求出符合下列条件的实数 的取值范围.
的取值范围.
(1)p、q至少有一个是真命题;(2)p∨q是真命题且p∧q是假命题.
【解析】本试题主要考查了函数的单调性,不等式的解集,以及命题的真值判定的综合运用。
查看答案和解析>>
科目:高中数学 来源:安徽省蚌埠二中2013届高二下学期期中考试文科数学试卷(解析版) 题型:解答题
命题p:关于 的不等式
的不等式 的解集为
的解集为 ;
;
命题q:函数 为增函数.
为增函数.
分别求出符合下列条件的实数 的取值范围.
的取值范围.
(1)p、q至少有一个是真命题;(2)p∨q是真命题且p∧q是假命题.
【解析】本试题主要考查了函数的单调性,不等式的解集,以及命题的真值判定的综合运用。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com