
【题目】给出以下命题,其中真命题的个数是( )
①若“![]() 或
或![]() ”是假命题,则“
”是假命题,则“![]() 且
且![]() ”是真命题;
”是真命题;
②命题“若![]() ,则
,则![]() 或
或![]() ”为真命题;
”为真命题;
③已知空间任意一点![]() 和不共线的三点
和不共线的三点![]() ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 四点共面;
四点共面;
④直线![]() 与双曲线
与双曲线![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() ,则这样的直线有3条;
,则这样的直线有3条;
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】(1)若“![]() 或
或![]() ”是假命题,则
”是假命题,则![]() 是假命题p是真命题,
是假命题p是真命题,![]() 是假命题
是假命题![]() 是真命题,故
是真命题,故![]() 且
且![]() 真命题,选项正确.
真命题,选项正确.
(2) 命题“若![]() ,则
,则![]() 或
或![]() ”的逆否命题是若a=2,且b=3,则a+b=5.这个命题是真命题,故原命题也是真命题.
”的逆否命题是若a=2,且b=3,则a+b=5.这个命题是真命题,故原命题也是真命题.
(3)∵![]() +
+![]() +
+![]() =1,∴P,A,B,C四点共面,故(3)正确,
=1,∴P,A,B,C四点共面,故(3)正确,
(4)由双曲线方程得a=2,c=3,即直线l:y=k(x﹣3)过双曲线的右焦点,
∵双曲线的两个顶点之间的距离是2a=4,a+c=2+3=5,
∴当直线与双曲线左右两支各有一个交点时,当k=0时2a=4,
则满足|AB|=5的直线有2条,当直线与实轴垂直时,
当x=c=3时,得![]() ,即
,即![]() =
=![]() ,即则y=±
,即则y=±![]() ,
,
此时通径长为5,若|AB|=5,则此时直线AB的斜率不存在,故不满足条件.综上可知有2条直线满足|AB|=5,故(4)错误,
故答案为:C.


科目:高中数学 来源: 题型:
【题目】北京市某年11月1日—20日监测最高最低温度及差值数据如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
最高温度(℃) | 20 | 16 | 14 | 20 | 20 | 20 | 18 | 15 | 12 | 11 | 12 | 12 | 13 | 9 | 8 | 6 | 13 | 11 | 10 | 14 |
最低温度(℃) | 5 | 4 | 2 | 4 | 9 | 6 | 9 | 3 | -1 | 0 | 5 | 1 | 4 | -1 | -4 | -2 | -1 | 0 | 1 | 3 |
差值(℃) | 15 | 12 | 12 | 16 | 11 | 14 | 9 | 12 | 13 | 11 | 7 | 11 | 9 | 10 | 12 | 8 | 14 | 11 | 9 | 11 |
(Ⅰ)完成下面的频率分布表及频率分布直方图,并写出频率分布直方图中![]() 的值;
的值;

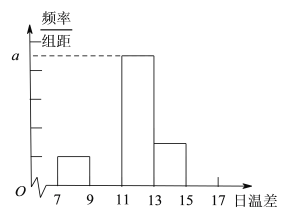
(Ⅱ)从日温差大于等于![]() 的这些天中,随机选取2天.求这两天中至少有一天的温差在区间
的这些天中,随机选取2天.求这两天中至少有一天的温差在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[100,110),[110,120),[120,130)三组内的学生中,用分层抽样的方法选取28人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在去年的足球甲![]() 联赛上,一队每场比赛平均失球数是1.5,全年比赛失球个数的标准差为1.1;二队每场比赛平均失球数是2.1,全年失球个数的标准差是0.4,你认为下列说法中正确的个数有( )
联赛上,一队每场比赛平均失球数是1.5,全年比赛失球个数的标准差为1.1;二队每场比赛平均失球数是2.1,全年失球个数的标准差是0.4,你认为下列说法中正确的个数有( )
①平均来说一队比二队防守技术好;②二队比一队防守技术水平更稳定;③一队防守有时表现很差,有时表现又非常好;④二队很少不失球.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(ax+ ![]() )+
)+ ![]() .
.
(1)若a>0,且f(x)在(0,+∞)上单调递增,求实数a的取值范围;
(2)是否存在实数a,使得函数f(x)在(0,+∞)上的最小值为1?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出一个问题的算法:
S1 输入x;
S2 若x≤2,则执行S3;否则,执行S4;
S3 输出-2x-1;
S4 输出x2-6x+3.
问题:
(1)这个算法解决的是什么问题?
(2)当输入的x值为多大时,输出的数值最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com