
【题目】如图,若Ω是长方体ABCD﹣A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1 , 则下列结论中不正确的是( )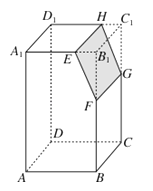
A.EH∥FG
B.四边形EFGH是矩形
C.Ω是棱柱
D.Ω是棱台
【答案】D
【解析】解:因为EH∥A1D1 , A1D1∥B1C1 ,
所以EH∥B1C1 , 又EH平面BCC1B1 , 平面EFGH∩平面BCC1B1=FG,
所以EH∥平面BCB1C1 , 又EH平面EFGH,
平面EFGH∩平面BCB1C1=FG,
所以EH∥FG,故EH∥FG∥B1C1 ,
所以选项A、C正确;
因为A1D1⊥平面ABB1A1 ,
EH∥A1D1 , 所以EH⊥平面ABB1A1 ,
又EF平面ABB1A1 , 故EH⊥EF,所以选项B也正确,
故选D.
根据直线与平面平行的性质定理可知EH∥FG,则EH∥FG∥B1C1 , 从而Ω是棱柱,因为A1D1⊥平面ABB1A1 , EH∥A1D1 , 则EF⊥平面ABB1A1 , 又EF平面ABB1A1 , 故EH⊥EF,从而四边形EFGH是矩形.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:
【题目】已知x∈R,符号[x]表示不超过x的最大整数,若函数f(x)=![]() (x>0),则给出以下四个结论:
(x>0),则给出以下四个结论:
①函数f(x)的值域为[0,1];
②函数f(x)的图象是一条曲线;
③函数f(x)是(0,+∞)上的减函数;
④函数g(x)=f(x)﹣a有且仅有3个零点时![]() .
.
其中正确的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用min{a,b,c}表示a,b,c三个数中的最小值,设f(x)=min{2x , x+2,10﹣x}(x≥0),则f(x)的最大值为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论不正确的是( )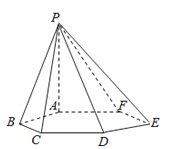
A.CD∥平面PAF
B.DF⊥平面PAF
C.CF∥平面PAB
D.CF⊥平面PAD
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线a上的所有点到两条直线m、n的距离都相等,则称直线a为“m、n的等距线”.在正方体ABCD﹣A1B1C1D1中,E、F、G、H分别是所在棱中点,M、N分别为EH、FG中点,则在直线MN,EG,FH,B1D中,是“A1D1、AB的等距线”的条数为( )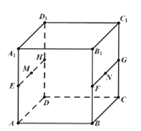
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 上的最大值为
上的最大值为![]() ,求实数
,求实数![]() 的值;
的值;
(2)若对任意![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)在(1)的条件下,设![]() ,对任意给定的正实数
,对任意给定的正实数![]() ,曲线
,曲线![]() 上是否存在两点
上是否存在两点![]() 、
、![]() ,使得
,使得![]() 是以
是以![]() (
(![]() 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在![]() 轴上?请说明理由。
轴上?请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (x﹣2)的定义域为集合A,函数
(x﹣2)的定义域为集合A,函数![]() 的值域为集合B.
的值域为集合B.
(1)求A∪B;
(2)若集合C={x|a≤x≤3a﹣1},且B∩C=C,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com