
分析 (1)若a=-1,由绝对值的意义求得不等式f(x)≥3的解集.
(2)由条件利用绝对值的意义求得函数f(x)的最小值为|a-1|,可得|a-1|=2,由此求得a的值.
解答 解:(1)若a=-1,函数f(x)=|x-1|+|x-a|=|x-1|+|x+1|,表示数轴上的x对应点到1、-1对应点的距离之和,
而-1.2和 1.5 对应点到1、-1对应点的距离之和正好等于3,
故不等式f(x)≥3的解集为{x|≤-1.5,或 x≥1.5}.
(2)由于?x∈R,f(x)≥2,故函数f(x)的最小值为2.
函数f(x)=|x-1|+|x-a|表示数轴上的x对应点到1、a对应点的距离之和,它的最小值为|a-1|,
即|a-1|=2,求得a=3 或a=-1.
点评 本题主要考查绝对值的意义,函数的恒成立问题,属于中档题.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{16}$ | B. | -$\frac{1}{16}$ | C. | $\frac{11}{16}$ | D. | -$\frac{11}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{8}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | “合情推理”的下位 | B. | “直接证明”的下位 | ||
| C. | “演绎推理”的下位 | D. | “间接证明”的下位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
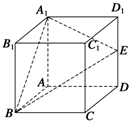 如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.
如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{40}{3}$ | B. | $\frac{28}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com