
����Ŀ��ij����ѧԺ2018����ɽ�����������������ܶ�.������Ա��ij��������ȡ�˸���2018�������������Գɼ���200��ѧ����ɫ�ʺ�����ij��Գɼ������ɼ����飬�õ���Ƶ�ʷֲ�������ͼ��ʾ.
��� | ���� | Ƶ�� | Ƶ�� |
��1�� |
| 24 | 0.12 |
��2�� |
| �� | 0.18 |
��3�� |
| 64 | 0.32 |
��4�� |
| 60 | �� |
��5�� |
| 16 | 0.08 |
�ϼ� | 200 | 1.00 | |
��1���������Ƶ�ʷֲ����Т١���λ����Ӧ���ݣ����ڴ���ֽ���������Ƶ�ʷֲ�ֱ��ͼ������Ƶ�ʷֲ�ֱ��ͼ������λ����
��2��Ϊ���ܸ�������˽����ѧ�������������Ժ�����ڸ�����ǰ�Ƚ��г�������.���ܳ��غͽ��������Ŀ����ƣ������ӵ�3��ѡ��3�ˣ���4��ѡ��2�ˣ���5��ѡ��1�ˣ�Ȼ�����6������ѡ��2�˽��е��У�����2�˾����Ե�����ĸ���.
���𰸡���1���ٴ���36���ڴ���0.30����ͼ����������λ��Ϊ173.125��2��![]()
��������
��1���ɸ�����������ݺ�Ϊ�����ֱ�����ٺ͢ڴ������ݣ�����Ƶ�ʺ�����Ƶ�ʷֲ�ֱ��ͼ��������λ����ߺ��ұߵ�ֱ��ͼ�����ȼ��������λ����
��2���о�![]() ���������ȡ
���������ȡ![]() �˵��ܵĻ����¼��������оٳ���
�˵��ܵĻ����¼��������оٳ���![]() �˾����Ե�����Ļ����¼��������ùŵ����ʽ������ý��.
�˾����Ե�����Ļ����¼��������ùŵ����ʽ������ý��.
��1�������⣬�ٴ�������Ϊ![]() ��
��
�ڴ�������Ϊ![]() ��
��
�ٴ���![]() ���ڴ���
���ڴ���![]() ��
��
Ƶ�ʷֲ�ֱ��ͼ���£�
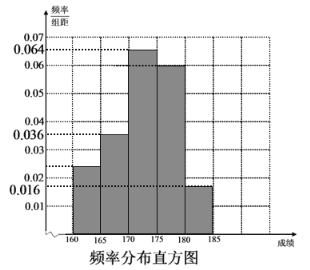
��ͼ֪��ǰ�������Ƶ�ʺ�Ϊ![]() ��ǰ�������Ƶ�ʺ�Ϊ
��ǰ�������Ƶ�ʺ�Ϊ![]() .
.
����λ���ڵ�![]() ���У���Ϊ
���У���Ϊ![]() ��
��
��![]() �����
�����![]() ��
��
����λ��Ϊ![]() ��
��
��2����ѡ����![]() ���У���
������![]() ���
���![]() �˼�Ϊ
�˼�Ϊ![]() ��
��![]() ��
��![]() ����
����![]() ���
���![]() �˼�Ϊ
�˼�Ϊ![]() ��
��![]() ����
����![]() ���
���![]() �˼�Ϊ
�˼�Ϊ![]() .
.
���ȡ![]() �����п��ܽ��Ϊ
�����п��ܽ��Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �֣�
�֣�
��![]()
![]() ѡ����
ѡ����![]() �˾����Ե�
�˾����Ե�![]() ��
��![]() ��
��
�¼�![]() �����п��ܽ��Ϊ
�����п��ܽ��Ϊ![]() ��
��![]() ��
��![]() ��
��![]() �֣�
�֣�
��![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̳�����ij����Ʒ�ľ������������Ʒÿ�յ�������![]() (��λ��ǧ��)�����ۼ۸�
(��λ��ǧ��)�����ۼ۸�![]() (��λ��Ԫ/ǧ��)�����ϵʽ
(��λ��Ԫ/ǧ��)�����ϵʽ![]() ������
������![]() ��
��![]() Ϊ��������֪���ۼ۸�Ϊ5Ԫ/ǧ��ʱ��ÿ�տ��۳�����Ʒ11ǧ�ˣ�
Ϊ��������֪���ۼ۸�Ϊ5Ԫ/ǧ��ʱ��ÿ�տ��۳�����Ʒ11ǧ�ˣ�
(1) ��![]() ��ֵ��
��ֵ��
(2) ����Ʒ�ij�ƷΪ3Ԫ/ǧ��, ��ȷ�����ۼ۸�![]() ��ֵ,ʹ�̳�ÿ�����۸���Ʒ����õ��������
��ֵ,ʹ�̳�ÿ�����۸���Ʒ����õ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .����
.����![]() .
.
��1�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��2������![]() ��
��![]() �����ڼ�ֵ��1����
�����ڼ�ֵ��1����![]() ʱ��
ʱ��![]() ���������ʵ��
���������ʵ��![]() ���������.
���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й��Ŵ���ѧ�����������������еġ���ݸ��������һ��������ݸ��������Ǹı�һ�⣺�����Ѳݵ�һ�쳤Ϊ���ߣ�ݸ�ݵ�һ�쳤Ϊһ�ߣ��Ժ��Ѳݵ���������������룬ݸ�ݵ�������������ӱ������ʼ����ݸ�ݵij������Ѳݵij��ȵ����������¸�����������ĸ��⣬�侫ȷ����ߵ��ǣ��������һλС�����ο����ݣ�lg2��0.30��lg3��0.48���� ��
A.2.6��B.3.0��C.3.6��D.4.0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ����ֳ���������ʱ������������в���100β�㣬�������ֱ���[4��4.5����[4.5.5����[5.5.5����[5.5��6����[6��6.5����[6.5��7]����λ����У���ͳ�Ƶ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ
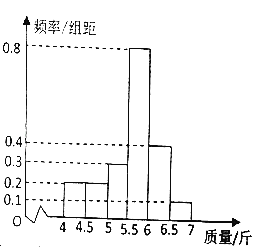
��1���ְ��ֲ�����ķ�����������Ϊ[4.5��5����[5��5.5�������������ȡ5β���ٴ���5β�������ȡ2β�����������X��ʾ������[4.5��5���ڵ����β������X�ķֲ��м���ѧ������
��2���Ը������ݵ��м��������������ݵ�ƽ��ֵ����Ƶ����Ϊ���ʣ�����ֳ����δ���̵����Լ����1000β����������������
����һ������ʣ�����������������������5.5������ۼ�Ϊÿ��10Ԫ����������5.5������ۼ�Ϊÿ��12Ԫ
��������һ�ܺ�����ʣ�������������������ÿβ����������䣬�����Ŀ���䣬��������5.5������ۼ�Ϊÿ��15Ԫ����������ֳһ�ܵķ�����ƽ��ÿβ22Ԫ����������5.5������ۼ�Ϊÿ��16Ԫ����������ֳһ�ܵķ�����ƽ��ÿβ24Ԫͨ������ȷ��ˮ����ֳ��ѡ�����ַ����������ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪m��n��������ͬ��ֱ�ߣ���������������ͬ��ƽ�棬�����������⣺
����m��n��n������m��������������
��������������������m��n��m����n������n������
����m������m��n��n����������������������
������������m��n��m��n����n������n������n������
������ȷ���������ǣ� ��
A.�٢�B.�٢�C.�٢�D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �Ƕ�����ʵ����R�ϵ��溯������������
�Ƕ�����ʵ����R�ϵ��溯������������![]() ���ǵ�����������
���ǵ�����������![]() ����
����![]() ��ȡֵ��ΧΪ_______��
��ȡֵ��ΧΪ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��![]() �Ƕ����ڣ���1��1���ϵ��溯������f��
�Ƕ����ڣ���1��1���ϵ��溯������f��![]() ��
��![]() ��
��
��1��ȷ�������Ľ���ʽ��
��2���ö��巨�жϺ����ĵ����ԣ�
��3���ⲻ��ʽ��f��t��1��+f��t����0.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com