
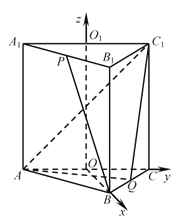
【题目】如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.

(1)求异面直线BP与AC1所成角的余弦值;
(2)求直线CC1与平面AQC1所成角的正弦值.
【答案】(1)![]()
(2)![]()
【解析】分析:(1)先建立空间直角坐标系,设立各点坐标,根据向量数量积求得向量![]() 的夹角,再根据向量夹角与异面直线所成角的关系得结果;(2)利用平面的方向量的求法列方程组解得平面
的夹角,再根据向量夹角与异面直线所成角的关系得结果;(2)利用平面的方向量的求法列方程组解得平面![]() 的一个法向量,再根据向量数量积得向量夹角,最后根据线面角与所求向量夹角之间的关系得结果.
的一个法向量,再根据向量数量积得向量夹角,最后根据线面角与所求向量夹角之间的关系得结果.
详解:如图,在正三棱柱ABCA1B1C1中,设AC,A1C1的中点分别为O,O1,则OB⊥OC,OO1⊥OC,OO1⊥OB,以![]() 为基底,建立空间直角坐标系Oxyz.
为基底,建立空间直角坐标系Oxyz.
因为AB=AA1=2,
所以![]() .
.
(1)因为P为A1B1的中点,所以![]() ,
,
从而![]() ,
,
故 .
.
因此,异面直线BP与AC1所成角的余弦值为![]() .
.
(2)因为Q为BC的中点,所以![]() ,
,
因此![]() ,
,![]() .
.
设n=(x,y,z)为平面AQC1的一个法向量,
则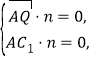 即
即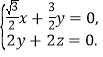
不妨取![]() ,
,
设直线CC1与平面AQC1所成角为![]() ,
,
则 ,
,
所以直线CC1与平面AQC1所成角的正弦值为![]() .
.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
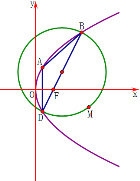
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过焦点
,过焦点![]() 且斜率存在的直线
且斜率存在的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,且
两点,且![]() 点在
点在![]() 点上方,
点上方,![]() 点与
点与![]() 点关于
点关于![]() 轴对称.
轴对称.
(1)求证:直线![]() 过某一定点
过某一定点![]() ;
;
(2)当直线![]() 的斜率为正数时,若以
的斜率为正数时,若以![]() 为直径的圆过
为直径的圆过![]() ,求
,求![]() 的内切圆与
的内切圆与![]() 的外接圆的半径之比.
的外接圆的半径之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面四边形![]() 中(如图1),
中(如图1),![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,且
,且![]() ,
,![]() ,现将此平面四边形沿
,现将此平面四边形沿![]() 折起使二面角
折起使二面角![]() 为直二面角,得到立体图形(如图2),又
为直二面角,得到立体图形(如图2),又![]() 为平面
为平面![]() 内一点,并且
内一点,并且![]() 为正方形,设
为正方形,设![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.
的中点.
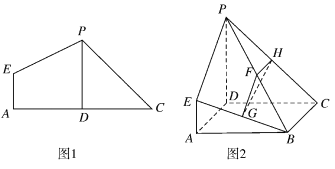
(Ⅰ)求证:面![]() 面
面![]() ;
;
(Ⅱ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得面
,使得面![]() 与面
与面![]() 所成二面角的余弦值为
所成二面角的余弦值为![]() ?若存在,求线段
?若存在,求线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是奇函数.
是奇函数.
(1)求实数![]() 的值;
的值;
(2)若![]() ,对任意
,对任意![]() 有
有![]() 恒成立,求实数
恒成立,求实数![]() 取值范围;
取值范围;
(3)设![]() ,若
,若![]() ,问是否存在实数
,问是否存在实数![]() 使函数
使函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”已知l丈为10尺,该楔体的三视图如图所示,其中网格纸上小正方形边长为1,则该楔体的体积为( )
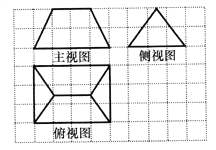
A. 10000立方尺 B. 11000立方尺
C. 12000立方尺 D. 13000立方尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场按月订购一种家用电暖气,每销售一台获利润200元,未销售的产品返回厂家,每台亏损50元,根据往年的经验,每天的需求量与当天的最低气温有关,如果最低气温位于区间![]() ,需求量为100台;最低气温位于区间
,需求量为100台;最低气温位于区间![]() ,需求量为200台;最低气温位于区间
,需求量为200台;最低气温位于区间![]() ,需求量为300台。公司销售部为了确定11月份的订购计划,统计了前三年11月份各天的最低气温数据,得到下面的频数分布表:
,需求量为300台。公司销售部为了确定11月份的订购计划,统计了前三年11月份各天的最低气温数据,得到下面的频数分布表:
最低气温(℃) |
|
|
|
|
|
天数 | 11 | 25 | 36 | 16 | 2 |
以最低气温位于各区间的频率代替最低气温位于该区间的概率.
求11月份这种电暖气每日需求量![]() (单位:台)的分布列;
(单位:台)的分布列;
若公司销售部以每日销售利润![]() (单位:元)的数学期望为决策依据,计划11月份每日订购200台或250台,两者之中选其一,应选哪个?
(单位:元)的数学期望为决策依据,计划11月份每日订购200台或250台,两者之中选其一,应选哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
| 6 |
| 7 | |
| 6 | 7 | 8 | |
| 5 | 6 | 7 | 8 |
(Ⅰ)试估计![]() 班学生人数;
班学生人数;
(Ⅱ)从![]() 班和
班和![]() 班抽出来的学生中各选一名,记
班抽出来的学生中各选一名,记![]() 班选出的学生为甲,
班选出的学生为甲,![]() 班选出的学生为乙,若学生锻炼相互独立,求甲的锻炼时间大于乙的锻炼时间的概率.
班选出的学生为乙,若学生锻炼相互独立,求甲的锻炼时间大于乙的锻炼时间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com