
| A. | $\frac{3}{2}$ | B. | 3 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
分析 确定双曲线$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1的右顶点的坐标,渐近线方程,利用点到直线的距离公式,即可求得结论.
解答 解:双曲线$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1的渐近线方程为y=±$\frac{\sqrt{3}}{3}x$,即x±$\sqrt{3}$y=0,右顶点A(2$\sqrt{3}$,0),
∴点A到该双曲线的一条渐近线的距离是$\frac{2\sqrt{3}}{\sqrt{1+3}}$=$\sqrt{3}$.
故选:D.
点评 本题考查双曲线的几何性质,考查点到直线的距离公式,确定双曲线的右顶点的坐标,渐近线方程是关键.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{10}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 过抛物线x2=-2py焦点的直线被抛物线截得的最短弦长为2p | |
| B. | 命题“有些自然数是偶数”是特称命题 | |
| C. | 离心率为$\sqrt{2}$的双曲线的两渐近线互相垂直 | |
| D. | 对于空间向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,则有($\overrightarrow{a}$•$\overrightarrow{b}$)$\overrightarrow{c}$=$\overrightarrow{a}$($\overrightarrow{b}$•$\overrightarrow{c}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
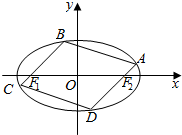 已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),两点F1(-1,0)、F2(1,0)为椭圆C的焦点,点P在椭圆C上,且|PF1|+|PF2|=2|F1F2|.
已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),两点F1(-1,0)、F2(1,0)为椭圆C的焦点,点P在椭圆C上,且|PF1|+|PF2|=2|F1F2|.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
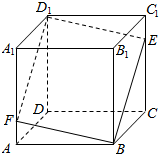 如图所示,在正方体ABCD-A1B1C1D1中,点E是棱CC1上的一个动点,平面BED1交棱AA1于点F.则下列命题中真命题的个数是( )
如图所示,在正方体ABCD-A1B1C1D1中,点E是棱CC1上的一个动点,平面BED1交棱AA1于点F.则下列命题中真命题的个数是( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com