
【题目】选修4-4:坐标系与参数方程
已知![]() ,在直角坐标系
,在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数);在以坐标原点
为参数);在以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)设点![]() 的极坐标为
的极坐标为![]() ,
, ![]() 为直线
为直线![]() ,
, ![]() 的交点,求
的交点,求![]() 的最大值.
的最大值.
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】如图,气象部门预报,在海面上生成了一股较强台风,在据台风中心60千米的圆形区域内将受到严重破坏,台风中心这个从海岸M点登陆,并以72千米/小时的速度沿北偏西60°的方向移动,已知M点位于A城的南偏东15°方向,距A城 ![]() 千米;M点位于B城的正东方向,距B城
千米;M点位于B城的正东方向,距B城 ![]() 千米,假设台风在移动的过程中,其风力和方向保持不变,请回答下列问题:
千米,假设台风在移动的过程中,其风力和方向保持不变,请回答下列问题: 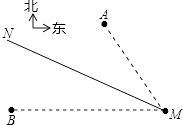
(1)A城和B城是否会受到此次台风的侵袭?并说明理由;
(2)若受到此次台风的侵袭,改城受到台风侵袭的持续时间有多少小时?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示. ![]() 是等腰梯形,
是等腰梯形, ![]() 米,
米, ![]() (
(![]() 在
在![]() 的延长线上,
的延长线上, ![]() 为锐角). 圆
为锐角). 圆![]() 与
与![]() 都相切,且其半径长为
都相切,且其半径长为![]() 米.
米. ![]() 是垂直于
是垂直于![]() 的一个立柱,则当
的一个立柱,则当![]() 的值设计为多少时,立柱
的值设计为多少时,立柱![]() 最矮?
最矮?
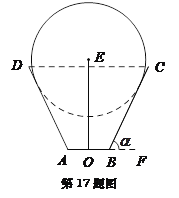
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() (
(![]() ),设
),设![]() 为圆
为圆![]() 与
与![]() 轴负半轴的交点,过点
轴负半轴的交点,过点![]() 作圆
作圆![]() 的弦
的弦![]() ,并使弦
,并使弦![]() 的中点恰好落在
的中点恰好落在![]() 轴上.
轴上.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)延长![]() 交曲线
交曲线![]() 于点
于点![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 交于点
交于点![]() ,试判断以点
,试判断以点![]() 为圆心,线段
为圆心,线段![]() 长为半径的圆与直线
长为半径的圆与直线![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第96届(春季)全国糖酒商品交易会于2017年3月23日至25日在四川举办.交易会开始前,展馆附近一家川菜特色餐厅为了研究参会人数与餐厅所需原材料数量的关系,查阅了最近5次交易会的参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下数据:
(袋),得到如下数据:

(Ⅰ)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() 投入使用的每袋原材料相应的销售收入为600元,多余的原材料只能无偿返还.若餐厅原材料现恰好用完,据悉本次交易会大约有14万人参加,根据(Ⅰ)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润
投入使用的每袋原材料相应的销售收入为600元,多余的原材料只能无偿返还.若餐厅原材料现恰好用完,据悉本次交易会大约有14万人参加,根据(Ⅰ)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
(参考公式: 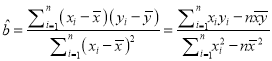 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点到准线的距离为
的焦点到准线的距离为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线![]() 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点![]() .
.
(1)若![]() 的坐标为
的坐标为![]() ,求
,求![]() 的值;
的值;
(2)设线段![]() 的中点为
的中点为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,过
,过![]() 的直线
的直线![]() 与线段
与线段![]() 为直径的圆相切,切点为
为直径的圆相切,切点为![]() ,且直线
,且直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,证明:
两点,证明:  .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com