
分析 (1)由ρ2=x2+y2,ρcosθ=x,ρsinθ=y,能求出曲线的直角坐标方程;由三角函数的关系求出直线l的参数方程即可;
(2)利用韦达定理和弦长公式能求出|PA|•|PB|及|PC|•|PD|的值,从而证出结论.
解答 解:(1)∵E的极坐标方程为$ρ=\frac{4tanθ}{cosθ}$,
∴ρ2cos2θ=4ρsinθ,
∴E:x2=4y(x≠0),
∴倾斜角为α的直线l过点P(2,2),
∴l:$\left\{\begin{array}{l}x=2+tcosα\\ y=2+tsinα\end{array}\right.$(t为参数) (5分)
(2)∵l1,l2关于直线x=2对称,
∴l1,l2的倾斜角互补.设l1的倾斜角为α,则l2的倾斜角为π-α,
把直线l1:$\left\{\begin{array}{l}x=2+tcosα\\ y=2+tsinα\end{array}\right.$(t为参数)代入x2=4y并整理得:
t2cos2α+4(cosα-sinα)t-4=0,
根据韦达定理,t1t2=$-\frac{4}{{{{cos}^2}α}}$,即|PA|×|PB|=$\frac{4}{{{{cos}^2}α}}$.(8分)
同理即|PC|×|PD|=$\frac{4}{{{{cos}^2}(π-α)}}$=$\frac{4}{{{{cos}^2}α}}$.
∴|PA|×|PB|=|PC|×|PD|,
即|PA|:|PD|=|PC|:|PB|.(10分)
点评 本题考查曲线的极坐标方程化为直角坐标方程的应用,考查|PA|•|PB|及直线的倾斜角α的值的求法,是中题,解题时要注意韦达定理和弦长公式的合理应用.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有两个面平行,其余各面都是四边形,并且每相邻的两个四边形的公共边都互相平行的几何体叫棱柱 | |
| B. | 圆锥的过轴的截面是一个等腰三角形 | |
| C. | 直角三角形绕它的一条边旋转一周形成的曲面围成的几何体是圆锥 | |
| D. | 圆台平行于底面的截面是圆面 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
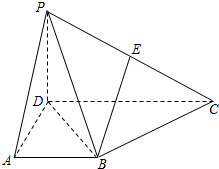 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{f(a)+f(b)}{2}$>$\frac{f(b)-f(a)}{b-a}$ | B. | $\frac{f(a)+f(b)}{2}$=$\frac{f(b)-f(a)}{b-a}$ | C. | $\frac{f(a)+f(b)}{2}$<$\frac{f(b)-f(a)}{b-a}$ | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{y^2}{16}-\frac{x^2}{9}=1$ | B. | $\frac{y^2}{16}-\frac{x^2}{9}=-1$ | C. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{16}-\frac{y^2}{9}=-1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com