
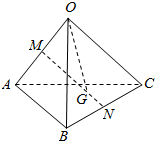
 如图,在三棱锥O-ABC中,M,N分别是棱OA、CB的中点,点G在线段MN上,且MG=2GN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,$\overrightarrow{OC}$=c.
如图,在三棱锥O-ABC中,M,N分别是棱OA、CB的中点,点G在线段MN上,且MG=2GN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,$\overrightarrow{OC}$=c.分析 (1)由题意结合平面向量的加减法运算求得$\overrightarrow{MN}$和$\overrightarrow{OG}$;
(2)把(1)中的$\overrightarrow{MN}$和$\overrightarrow{OG}$利用多项式乘多项式展开,再结合数量积公式求值.
解答 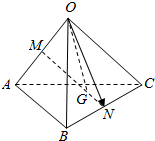 解:(1)如图,连接ON,∵M,N分别是棱OA、CB的中点,且MG=2GN,
解:(1)如图,连接ON,∵M,N分别是棱OA、CB的中点,且MG=2GN,
∴$\overrightarrow{MN}=\overrightarrow{ON}-\overrightarrow{OM}$=$\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})-\frac{1}{2}\overrightarrow{OA}$=$\frac{1}{2}(\overrightarrow{b}+\overrightarrow{c}-\overrightarrow{a})$.
$\overrightarrow{OG}=\overrightarrow{OM}+\overrightarrow{MG}$=$\frac{1}{2}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{MN}$=$\frac{1}{2}\overrightarrow{a}+\frac{2}{3}×\frac{1}{2}(\overrightarrow{b}+\overrightarrow{c}-\overrightarrow{a})$=$\frac{1}{3}(\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})$;
(2)∵OA=0B=OC=2,且∠AOB=∠BOC=60°,∠AOC=90°,
∴$\overrightarrow{MN}$•$\overrightarrow{OG}$=$\frac{1}{2}(\overrightarrow{b}+\overrightarrow{c}-\overrightarrow{a})•\frac{1}{3}(\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})$
=$\frac{1}{6}|\overrightarrow{b}{|}^{2}+\frac{1}{6}|\overrightarrow{c}{|}^{2}-\frac{1}{12}|\overrightarrow{a}{|}^{2}$$-\frac{1}{12}\overrightarrow{a}•\overrightarrow{b}+\frac{1}{3}\overrightarrow{b}•\overrightarrow{c}-\frac{1}{12}\overrightarrow{a}•\overrightarrow{c}$
=$\frac{1}{6}×4+\frac{1}{6}×4-\frac{1}{12}×4-\frac{1}{12}×2×2cos60°+\frac{1}{3}×2×2cos60°$
=1$-\frac{1}{3}×\frac{1}{2}$$+\frac{1}{3}×2$=$\frac{3}{2}$.
点评 本题考查平面向量的数量积运算,考查了向量的加减混合运算及其几何意义,考查计算能力,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com