Question

已知函数f(x)＝lg(a^x－b^x)(a>1>b>0)．

(1)求y＝f(x)的定义域；

(2)在函数y＝f(x)的图象上是否存在不同的两点，使得过这两点的直线平行于x轴；

(3)当a，b满足什么条件时，f(x)在(1，＋∞)上恒取正值．

 

Answer 1

【答案】

(1) f(x)的定义域是(0，＋∞)．

(2)函数y＝f(x)的图象上不存在不同两点，使过这两点的直线平行于x轴．

(3)当a≥b＋1时，f(x)在(1，＋∞)上恒取正值．

【解析】

试题分析：(1)由a^x－b^x>0得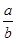（）^x>1，

∵a>1>b>0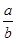，∴>1，∴x>0.

∴f(x)的定义域是(0，＋∞)．

(2)任取x₁、x₂∈(0，＋∞)且x₁>x₂，

∵a>1>b>0，∴ax₁>ax₂>1，bx₁<bx₂<1

∴ax₁－bx₁>ax₂－bx₂>0

∴lg(ax₁－bx₁)>lg(ax₂－bx₂)

故f(x₁)>f(x₂)

∴f(x)在(0，＋∞)上为增函数．

假设y＝f(x)的图象上存在不同的两点A(x₁，y₁)，B(x₂，y₂)，使过A、B两点的直线平行于x轴，则x₁≠x₂，y₁＝y₂，这与f(x)是增函数矛盾．故函数y＝f(x)的图象上不存在不同两点，使过这两点的直线平行于x轴．

(3)∵f(x)是增函数，∴当x∈(1，＋∞)时，f(x)>f(1)．

这样只需f(1)≥0，即lg(a－b)≥0，

∴a－b≥1.

即当a≥b＋1时，f(x)在(1，＋∞)上恒取正值．

考点：对数函数的性质，函数的单调性，函数的图象，不等式恒成立问题。

点评：中档题，本题综合性较强，较全面的考查函数的图象和性质。不等式的恒成立问题，往往通过研究函数的单调性及最值，使问题得到解决。本题研究函数的单调性，主要利用了增（减）函数的定义，遵循“设，作差，变形，定号，结论”等加以研究。