
【题目】已知![]() 中,角
中,角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,________.是否存在以
,________.是否存在以![]() ,
,![]() ,
,![]() 为边的三角形?如果存在,求出
为边的三角形?如果存在,求出![]() 的面积;若不存在,说明理由.
的面积;若不存在,说明理由.
从①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选一个,补充在上面问题中并作答.
这三个条件中任选一个,补充在上面问题中并作答.
【答案】详见解析
【解析】
若选取条件①![]() ,可先求出
,可先求出![]() 的值,进而由余弦定理
的值,进而由余弦定理![]() ,可出
,可出![]() 的值,进而结合
的值,进而结合![]() ,可求出
,可求出![]() 的值,从而可判断该三角形存在,进而求出三角形的面积即可;
的值,从而可判断该三角形存在,进而求出三角形的面积即可;
若选取条件②,由余弦定理![]() ,可出
,可出![]() 的值,进而结合
的值,进而结合![]() ,可求得
,可求得![]() ,从而可知该三角形不存在;
,从而可知该三角形不存在;
若选取条件③![]() ,可得
,可得![]() ,进而分两种情况,分别讨论即可.
,进而分两种情况,分别讨论即可.
若选取条件①![]() ,此时
,此时![]() ,
,
因为![]() ,所以
,所以![]() ,
,
由余弦定理,![]() ,解得
,解得![]() ,
,
则![]() ,所以
,所以![]() ,
,
所以![]() ,又
,又![]() ,解得
,解得![]() 或者
或者![]() ,
,
所以存在以![]() ,
,![]() ,
,![]() 为边的三角形,其面积为
为边的三角形,其面积为![]() .
.
若选取条件②![]() ,
,
因为![]() ,所以
,所以![]() ,
,
由余弦定理,![]() ,解得
,解得![]() ,
,
则![]() ,所以
,所以![]() ,显然不成立,所以不存在以
,显然不成立,所以不存在以![]() ,
,![]() ,
,![]() 为边的三角形.
为边的三角形.
若选取条件③![]() ,得
,得![]() ,
,
由选取条件①可知,当![]() 时,存在以
时,存在以![]() ,
,![]() ,
,![]() 为边的三角形,其面积为
为边的三角形,其面积为![]() .
.
由选取条件②可知,当![]() 时,不存在以
时,不存在以![]() ,
,![]() ,
,![]() 为边的三角形.
为边的三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》中有一题:今有牛、马、羊食人苗,苗主责之粟四斗.羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?其意是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿4斗粟,羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比率偿还,牛、马、羊的主人各应赔偿多少粟?在这个问题中,牛主人比羊主人多赔偿了多少斗( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定数列![]() .对
.对![]() ,该数列前
,该数列前![]() 项
项![]() 的最小值记为
的最小值记为![]() ,后
,后![]() 项
项![]() 的最大值记为
的最大值记为![]() ,令
,令![]() .
.
(1)设数列![]() 为2,1,6,3,写出
为2,1,6,3,写出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)设![]() 是等比数列,公比
是等比数列,公比![]() ,且
,且![]() ,证明:
,证明:![]() 是等比数列;
是等比数列;
(3)设![]() 是公差大于0的等差数列,且
是公差大于0的等差数列,且![]() ,证明:
,证明:![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,证明:函数
时,证明:函数![]() 无零点;
无零点;
(3)确定![]() 的所有可能取值,使得
的所有可能取值,使得![]() 在区间
在区间![]() 内恒成立.
内恒成立.
(4)数学题目虽然千变万化,有很多形式虽然陌生新颖,但仔细分析其条件后又可以转换为若干熟悉的老问题,使新问题得以解决.因此,会将新问题转化为老问题的思想方法是学好数学的重要方法之一.下面你将问题(3)中的条件“![]() 在区间
在区间![]() 内恒成立”变化为两种新形式(不作解答).
内恒成立”变化为两种新形式(不作解答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,四边形
中,四边形![]() 为正方形,
为正方形,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点.
中点.
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/18/2487522753945600/2488179565404160/STEM/3bba3a8519b8447aaec6f2ca7eb73ba0.png]
(1)证明:![]() 平面
平面![]() ;
;
(2)已知![]() ,
,![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]() (s为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(s为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,
,![]() ,直线与曲线C交于A,B两点.
,直线与曲线C交于A,B两点.
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)已知点P的极坐标为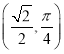 ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com