
【题目】函数![]() ,且
,且![]() 恒成立.
恒成立.
(1)求实数![]() 的集合
的集合![]() ;
;
(2)当![]() 时,判断
时,判断![]() 图象与
图象与![]() 图象的交点个数,并证明.
图象的交点个数,并证明.
(参考数据:![]() )
)
【答案】(1)![]() ;(2)2个,证明见解析
;(2)2个,证明见解析
【解析】
(1)要![]() 恒成立,只要
恒成立,只要![]() 的最小值大于或等于零即可,所以只要讨论求解看
的最小值大于或等于零即可,所以只要讨论求解看![]() 是否有最小值;
是否有最小值;
(2)将![]() 图像与
图像与![]() 图像的交点个数转化为方程
图像的交点个数转化为方程![]() 实数解的个数问题,然后构造函数
实数解的个数问题,然后构造函数![]() ,再利用导数讨论此函数零点的个数.
,再利用导数讨论此函数零点的个数.
(1)![]() 的定义域为
的定义域为![]() ,因为
,因为![]() ,
,
1°当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() 时,使得
时,使得![]() ,与条件矛盾;
,与条件矛盾;
2°当![]() 时,由
时,由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,即有
上单调递增,即有![]() ,由
,由![]() 恒成立,所以
恒成立,所以![]() 恒成立,令
恒成立,令![]() ,
,
若![]() ;
;
若![]() ;而
;而![]() 时,
时,![]() ,要使
,要使![]() 恒成立,
恒成立,
故![]() .
.
(2)原问题转化为方程![]() 实根个数问题,
实根个数问题,
当![]() 时,
时,![]() 图象与
图象与![]() 图象有且仅有2个交点,理由如下:
图象有且仅有2个交点,理由如下:
由![]() ,即
,即![]() ,令
,令![]() ,
,
因为![]() ,所以
,所以![]() 是
是![]() 的一根;
的一根;![]() ,
,
1°当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,
上单调递减,![]() ,即
,即![]() 在
在![]() 上无实根;
上无实根;
2°当![]() 时,
时,![]() ,
,
则![]() 在
在![]() 上单调递递增,又
上单调递递增,又![]() ,
,
所以![]() 在
在![]() 上有唯一实根
上有唯一实根![]() ,且满足
,且满足![]() ,
,
①当![]() 时,
时,![]() 在
在![]() 上单调递减,此时
上单调递减,此时![]() 在
在![]() 上无实根;
上无实根;
②当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,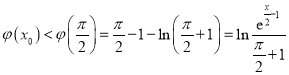
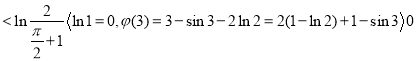 ,故
,故![]() 在
在![]() 上有唯一实根.
上有唯一实根.
3°当![]() 时,由(1)知,
时,由(1)知,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,
,
故![]() ,所以
,所以![]() 在
在![]() 上无实根.
上无实根.
综合1°,2°,3°,故![]() 有两个实根,即
有两个实根,即![]() 图象与
图象与![]() 图象有且仅有2个交点.
图象有且仅有2个交点.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】如图①,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=![]() CD=1.现以AD为一边向梯形外作正方形ADEF,然后沿边AD将正方形ADEF翻折,使平面ADEF与平面ABCD垂直,M为ED的中点,如图②.
CD=1.现以AD为一边向梯形外作正方形ADEF,然后沿边AD将正方形ADEF翻折,使平面ADEF与平面ABCD垂直,M为ED的中点,如图②.
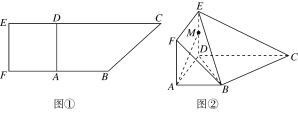
(1)求证:AM∥平面BEC;
(2)求点D到平面BEC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]()
![]() 交于
交于![]() 两点.
两点.
(1)求![]() 的长;
的长;
(2)在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立的极坐标系中,设点
轴的正半轴为极轴建立的极坐标系中,设点![]() 的极坐标为
的极坐标为![]() ,求点
,求点![]() 到线段
到线段![]() 中点
中点![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ,
,![]() )的图象如图所示,令
)的图象如图所示,令![]() ,则下列关于函数
,则下列关于函数![]() 的说法中正确的是( )
的说法中正确的是( )
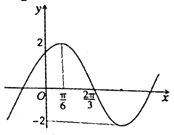
A. 函数![]() 图象的对称轴方程为
图象的对称轴方程为![]()
![]()
B. 函数![]() 的最大值为2
的最大值为2
C. 函数![]() 的图象上存在点
的图象上存在点![]() ,使得在
,使得在![]() 点处的切线与直线
点处的切线与直线![]() 平行
平行
D. 若函数![]() 的两个不同零点分别为
的两个不同零点分别为![]() ,
,![]() ,则
,则![]() 最小值为
最小值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是国家统计局于2020年1月9日发布的2018年12月到2019年12月全国居民消费价格的涨跌幅情况折线图.(注:同比是指本期与同期作对比;环比是指本期与上期作对比.如:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比)根据该折线图,下列结论错误的是( )
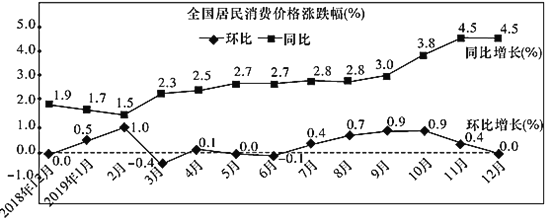
A.2019年12月份,全国居民消费价格环比持平
B.2018年12月至2019年12月全国居民消费价格环比均上涨
C.2018年12月至2019年12月全国居民消费价格同比均上涨
D.2018年11月的全国居民消费价格高于2017年12月的全国居民消费价格
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的图象经过点
的图象经过点![]() .
.
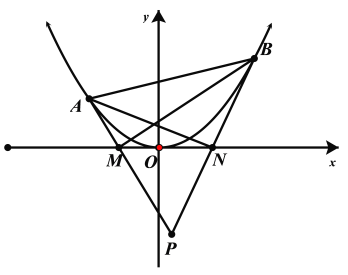
(1)求抛物线![]() 的方程和焦点坐标;
的方程和焦点坐标;
(2)直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 不同两点,且
不同两点,且![]() ,
,![]() 位于
位于![]() 轴两侧,过点
轴两侧,过点![]() ,
,![]() 分别作抛物线
分别作抛物线![]() 的两条切线交于点
的两条切线交于点![]() ,直线
,直线![]() ,
,![]() 与
与![]() 轴的交点分别记作
轴的交点分别记作![]() ,
,![]() .记
.记![]() 的面积为
的面积为![]() ,
,![]() 面积为
面积为![]() ,
,![]() 面积为
面积为![]() ,试问
,试问![]() 是否为定值,若是,请求出该定值;若不是,请说明理由.
是否为定值,若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为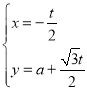 (
(![]() ,t为参数).以坐标原点为极点,
,t为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直角坐标系下直线![]() 与曲线
与曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 交于点
交于点![]() 、
、![]() (二者可重合),交
(二者可重合),交![]() 轴于
轴于![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情爆发以来,疫情防控牵挂着所有人的心. 某市积极响应上级部门的号召,通过沿街电子屏、微信公众号等各种渠道对此战“疫”进行了持续、深入的悬窗,帮助全体市民深入了解新冠状病毒,增强战胜疫情的信心. 为了检验大家对新冠状病毒及防控知识的了解程度,该市推出了相关的知识问卷,随机抽取了年龄在15~75岁之间的200人进行调查,并按年龄绘制频率分布直方图如图所示,把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年人”和“中老年人”. 经统计“青少年人”和“中老年人”的人数比为19:21. 其中“青少年人”中有40人对防控的相关知识了解全面,“中老年人”中对防控的相关知识了解全面和不够全面的人数之比是2:1.
内的人分别称为“青少年人”和“中老年人”. 经统计“青少年人”和“中老年人”的人数比为19:21. 其中“青少年人”中有40人对防控的相关知识了解全面,“中老年人”中对防控的相关知识了解全面和不够全面的人数之比是2:1.
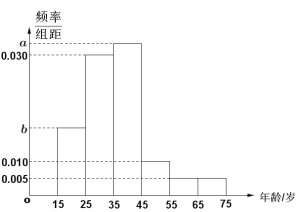
(1)求图中![]() 的值;
的值;
(2)现采取分层抽样在![]() 和
和![]() 中随机抽取8名市民,从8人中任选2人,求2人中至少有1人是“中老年人”的概率是多少?
中随机抽取8名市民,从8人中任选2人,求2人中至少有1人是“中老年人”的概率是多少?
(3)根据已知条件,完成下面的2×2列联表,并根据统计结果判断:能够有99.9%的把握认为“中老年人”比“青少年人”更加了解防控的相关知识?
了解全面 | 了解不全面 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
附表及公式: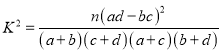 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图,90后从事互联网行业岗位分布条形图,则下列结论中不正确的是( )
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.


A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的![]()
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com