
分析 (1)确定所有基本事件个数,满足a≥b的事件数,然后直接利用古典概型概率计算公式求解;
(2)以x轴和y轴分别表示甲、乙两人到达约定地点的时间,若两人能够会面则|x-y|≤15.,由测度比是面积比求概率.
解答  解:(1)基本事件共有12个,其中a≥b基本事件包括(0,0),(1,1),(2,2),(1,0),(2,0),(2,1),(3,0),(3,1)(3,2)9个基本事件,所以a≥b的概率为:$\frac{9}{12}$=$\frac{3}{4}$;
解:(1)基本事件共有12个,其中a≥b基本事件包括(0,0),(1,1),(2,2),(1,0),(2,0),(2,1),(3,0),(3,1)(3,2)9个基本事件,所以a≥b的概率为:$\frac{9}{12}$=$\frac{3}{4}$;
(2)以x轴和y轴分别表示甲、乙两人到达约定地点的时间,若两人能够会面则|x-y|≤15.
在如图所示平面直角坐标系下,(x,y)的所有可能结果是边长为60的正方形区域,而事件A“两人能够会面”的可能结果由图中的阴影部分表示.由几何概型的概率公式得:P(A)=$\frac{6{0}^{2}-4{5}^{2}}{6{0}^{2}}$=$\frac{7}{16}$,所以,两人能会面的概率是$\frac{7}{16}$.
点评 本题考查了古典概型及其概率计算公式,考查了几何概型的概率,关键是理解(2)的测度比,是中档题.


科目:高中数学 来源: 题型:解答题
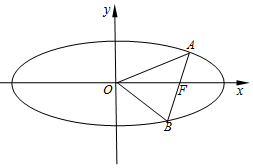 如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,过右焦点F的直线l交椭圆于A、B两点,当l与x轴垂直时,AB长为$\frac{{4\sqrt{3}}}{3}$.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,过右焦点F的直线l交椭圆于A、B两点,当l与x轴垂直时,AB长为$\frac{{4\sqrt{3}}}{3}$. 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>4} | B. | {x|x>0} | C. | {x|x<-1} | D. | {x|x>4或x<-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 0 | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com