

【题目】已知数列![]() 的奇数项是公差为
的奇数项是公差为![]() 的等差数列,偶数项是公差为
的等差数列,偶数项是公差为![]() 的等差数列,
的等差数列, ![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和, ![]()
(1)若![]() ,求
,求![]() ;
;
(2)已知![]() ,且对任意的
,且对任意的![]() ,有
,有![]() 恒成立,求证:数列
恒成立,求证:数列![]() 是等差数列;
是等差数列;
(3)若![]() ,且存在正整数
,且存在正整数![]() ,使得
,使得![]() ,求当
,求当![]() 最大时,数列
最大时,数列![]() 的通项公式.
的通项公式.
【答案】(1)14;(2)证明见解析;(3) 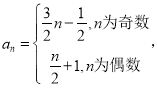
【解析】试题分析:
(1)利用题意求得公差,据此可得a10=14;
(2)结合(1)的结论证得d1=d2=2即可说明数列{an}是等差数列;
(3)分类讨论n的奇偶性即可得到数列的通项公式为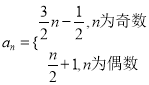 .
.
试题解析:
(1)根据题意,有a1=1,a2=2,a3=a1+d1=1+d1,a4=a2+d2=2+d2,a5=a3+d1=1+2d1∵S5=16,a4=a5
∴a1+a2+a3+a4+a5=7+3d1+d2=16,2+d2=1+2d1∴d1=2, d2=3.
∴a10=2+4d2=14
(2)证明:当n为偶数时,∵an<an+1恒成立,∴![]() ,
,
∴![]()
∴![]() 且d2>1
且d2>1
当n为奇数时,∵an<an+1恒成立,∴![]() ,
,
∴(1n)(d1d2)+2>0
∴![]()
∴d1=d2
∵S15=15a8,∴![]()
∴d1=d2=2
∴an=n
∴数列{an}是等差数列;
(3)若d1=3d2(d1≠0),且存在正整数m、n(m≠n),使得am=an,在m,n中必然一个是奇数,一个是偶数
不妨设m为奇数,n为偶数
∵am=an,∴![]()
∵d1=3d2,∴![]()
∵m为奇数,n为偶数,∴3mn1的最小正值为2,此时d1=3,d2=1
∴数列![]() 的通项公式为
的通项公式为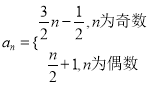 .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】迭代法是用于求方程或方程组近似根的一种常用的算法设计方法.设方程为![]() ,用某种数学方法到处等价的形式
,用某种数学方法到处等价的形式![]() ,然后按以下步骤执行:
,然后按以下步骤执行:
(1)选一个方程的近似根,赋给变量![]() ;
;
(2)将![]() 的值保存于变量
的值保存于变量![]() ,然后计算
,然后计算![]() ,并将结果存于变量
,并将结果存于变量![]() ;
;
(3)当![]() 与
与![]() 的差的绝对值还小于指定的精度要求时,重复步骤(2)的计算.若方程有根,则按上述方法求得的
的差的绝对值还小于指定的精度要求时,重复步骤(2)的计算.若方程有根,则按上述方法求得的![]() 就认为是方程的根.试用迭代法求某个数的平方根,用流程图和伪代码表示问题的算法.
就认为是方程的根.试用迭代法求某个数的平方根,用流程图和伪代码表示问题的算法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是二次函数,不等式
是二次函数,不等式![]() 的解集是
的解集是![]() ,且
,且![]() 在区间
在区间![]() 上的最大值是12.
上的最大值是12.
(1)求![]() 的解析式;
的解析式;
(2)是否存在自然数![]() ,使得方程
,使得方程![]() 在区间
在区间![]() 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
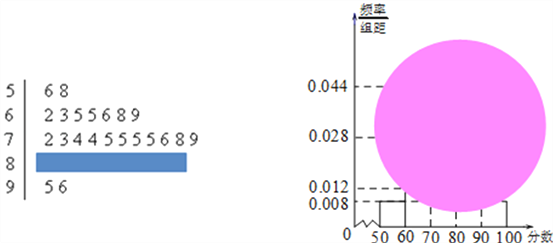
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高;
(Ⅲ)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90,100)之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要付出设备的维修和工人工资等费用![]() 的信息如下图.
的信息如下图.

(1)求![]() ;
;
(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了扩大该商品的影响力,提高年销售量,公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到![]() 元,公司拟投入
元,公司拟投入![]() 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入![]() 作为浮动宣传费用.试问:当该商品明年的销售量
作为浮动宣传费用.试问:当该商品明年的销售量![]() 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com