
【题目】已知关于x的一元二次不等式ax2+2x+b>0的解集为{x|x≠c},则![]() (其中a+c≠0)的取值范围为_____.
(其中a+c≠0)的取值范围为_____.
【答案】(﹣∞,﹣6]∪[6,+∞)
【解析】
由条件利用二次函数的性质可得ac=﹣1,ab=1, 即c=-b将![]() 转为(a﹣b)+
转为(a﹣b)+![]() ,利用基本不等式求得它的范围.
,利用基本不等式求得它的范围.
因为一元二次不等式ax2+2x+b>0的解集为{x|x≠c},由二次函数图像的性质可得a>0,二次函数的对称轴为x=![]() =c,△=4﹣4ab=0,
=c,△=4﹣4ab=0,
∴ac=﹣1,ab=1,∴c=![]() ,b=
,b=![]() ,即c=-b,
,即c=-b,
则![]() =
=![]() =(a﹣b)+
=(a﹣b)+![]() ,
,
当a﹣b>0时,由基本不等式求得(a﹣b)+![]() ≥6,
≥6,
当a﹣b<0时,由基本不等式求得﹣(a﹣b)﹣![]() ≥6,即(a﹣b)+
≥6,即(a﹣b)+![]() ≤﹣6,
≤﹣6,
故![]() (其中a+c≠0)的取值范围为:(﹣∞,﹣6]∪[6,+∞),
(其中a+c≠0)的取值范围为:(﹣∞,﹣6]∪[6,+∞),
故答案为:(﹣∞,﹣6]∪[6,+∞).


科目:高中数学 来源: 题型:
【题目】![]() 九章算术
九章算术![]() 是我国古代著名数学经典
是我国古代著名数学经典![]() 其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小
其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小![]() 以锯锯之,深一寸,锯道长一尺
以锯锯之,深一寸,锯道长一尺![]() 问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺
问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺![]() 问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示
问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示![]() 阴影部分为镶嵌在墙体内的部分
阴影部分为镶嵌在墙体内的部分![]() 已知弦
已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算该木材镶嵌在墙中的体积约为( )(注:1丈
寸,估算该木材镶嵌在墙中的体积约为( )(注:1丈![]() 尺
尺![]() 寸,
寸,![]() ,
,![]() )
)

A. 600立方寸 B. 610立方寸 C. 620立方寸 D. 633立方寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角坐标系![]() 中,点
中,点![]() 到抛物线
到抛物线![]() 的准线的距离为
的准线的距离为![]() ,点
,点![]() 是
是![]() 上的定点,
上的定点,![]() 、
、![]() 是
是![]() 上的两个动点,且线段
上的两个动点,且线段![]() 的中点
的中点![]() 在线段
在线段![]() 上.
上.
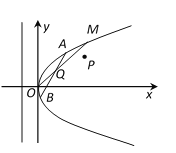
(1)抛物线![]() 的方程及
的方程及![]() 的值;
的值;
(2)当点![]() 、
、![]() 分别在第一、四象限时,求
分别在第一、四象限时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新中国成立70周年以来,党中央国务院高度重视改善人民生活,始终把提高人民生活水平作为一切工作的出发点和落脚点城乡居民收入大幅增长,居民生活发生了翻天覆地的变化.下面是1949年及2015年~2018年中国居民人均可支配收入(元)统计图.以下结论中不正确的是( )
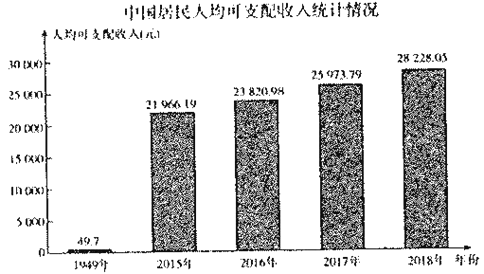
A.20l5年-2018年中国居民人均可支配收入与年份成正相关
B.2018年中居民人均可支配收入超过了1949年的500倍
C.2015年-2018年中国居民人均可支配收入平均超过了24000元
D.2015年-2018年中围居民人均可支配收入都超过了1949年的500倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列![]() 首项和公差都是
首项和公差都是![]() ,记
,记![]() 的前n项和为
的前n项和为![]() ,等比数列
,等比数列![]() 各项均为正数,公比为q,记
各项均为正数,公比为q,记![]() 的前n项和为
的前n项和为![]() :
:
(1)写出![]()
![]() 构成的集合A;
构成的集合A;
(2)若将![]() 中的整数项按从小到大的顺序构成数列
中的整数项按从小到大的顺序构成数列![]() ,求
,求![]() 的一个通项公式;
的一个通项公式;
(3)若q为正整数,问是否存在大于1的正整数k,使得![]()
![]() 同时为(1)中集合A的元素?若存在,写出所有符合条件的
同时为(1)中集合A的元素?若存在,写出所有符合条件的![]() 的通项公式,若不存在,请说明理由.
的通项公式,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它可应用到有限维空间,并构成一般不动点定理的基石.布劳威尔不动点定理得名于荷兰数学家鲁伊兹·布劳威尔(L.E. J. Brouwer),简单的讲就是对于满足一定条件的连续函数![]() ,存在一个点
,存在一个点![]() ,使得
,使得![]() ,那么我们称该函数为“不动点”函数,下列为“不动点”函数的是( )
,那么我们称该函数为“不动点”函数,下列为“不动点”函数的是( )
A.![]() B.
B.![]()
C.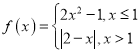 D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com