
【题目】已知△ABC的内角A、B、C的对边分别为a、b、c,且![]() .
.
(1)求A;
(2)若![]() ,求△ABC的面积S的最大值.
,求△ABC的面积S的最大值.
科目:高中数学 来源: 题型:
【题目】中国和印度是当今世界上两个发展最快且是最大的发展中国家,为了解两国经济的发展情况,收集了2008年至2017年两国GDP年度增长率,并绘制成如图折线图,则下列结论不正确的是( )
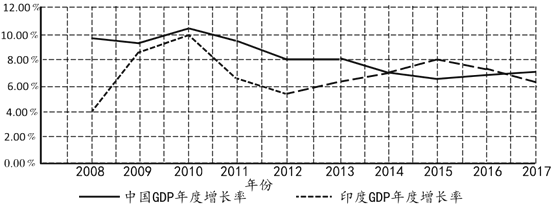
A.2010年,两国GDP年度增长率均为最大
B.2014年,两国GDP年度增长率几乎相等
C.这十年内,中国比印度的发展更为平稳一些
D.2015年起,印度GDP年度增长率均比中国大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() ,离心率
,离心率![]() ,短轴
,短轴![]() ,抛物线顶点在原点,以坐标轴为对称轴,焦点为
,抛物线顶点在原点,以坐标轴为对称轴,焦点为![]() ,
,
(1)求椭圆和抛物线的方程;
(2)设坐标原点为![]() ,
,![]() 为抛物线上第一象限内的点,
为抛物线上第一象限内的点,![]() 为椭圆是一点,且有
为椭圆是一点,且有![]() ,当线段
,当线段![]() 的中点在
的中点在![]() 轴上时,求直线
轴上时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,底面是边长为
中,底面是边长为![]() 的正三角形,点
的正三角形,点![]() 在底面
在底面![]() 上的射影
上的射影![]() 恰是
恰是![]() 的中点,侧棱
的中点,侧棱![]() 和底面成
和底面成![]() 角.
角.
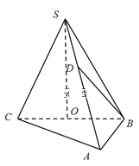
(1)若![]() 为侧棱
为侧棱![]() 上一点,当
上一点,当![]() 为何值时,
为何值时,![]() ;
;
(2)求二面角![]() 的余弦值大小.
的余弦值大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点E为正方形ABCD边CD上异于点C、D的动点,将△ADE沿AE翻折成△SAE,在翻折过程中,下列三个说法中正确的个数是( )
①存在点E和某一翻折位置使得AE∥平面SBC;
②存在点E和某一翻折位置使得SA⊥平面SBC;
③二面角S﹣AB﹣E的平面角总是小于2∠SAE.
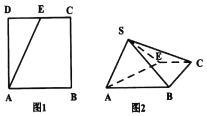
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现定义:设![]() 是非零实常数,若对于任意的
是非零实常数,若对于任意的![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 为“关于的
为“关于的![]() 偶型函数”
偶型函数”
(1)请以三角函数为例,写出一个“关于2的偶型函数”的解析式,并给予证明
(2)设定义域为的“关于的![]() 偶型函数”在区间
偶型函数”在区间![]() 上单调递增,求证在区间
上单调递增,求证在区间![]() 上单调递减
上单调递减
(3)设定义域为![]() 的“关于
的“关于![]() 的偶型函数”
的偶型函数”![]() 是奇函数,若
是奇函数,若![]() ,请猜测
,请猜测![]() 的值,并用数学归纳法证明你的结论
的值,并用数学归纳法证明你的结论
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】至![]() 年底,我国发明专利申请量已经连续
年底,我国发明专利申请量已经连续![]() 年位居世界首位,下表是我国
年位居世界首位,下表是我国![]() 年至
年至![]() 年发明专利申请量以及相关数据.
年发明专利申请量以及相关数据.
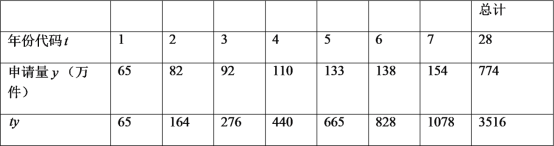
注:年份代码![]() ~
~![]() 分别表示
分别表示![]() ~
~![]() .
.
(1)可以看出申请量每年都在增加,请问这几年中哪一年的增长率达到最高,最高是多少?
(2)建立![]() 关于
关于![]() 的回归直线方程(精确到
的回归直线方程(精确到![]() ),并预测我国发明专利申请量突破
),并预测我国发明专利申请量突破![]() 万件的年份.
万件的年份.
参考公式:回归直线的斜率和截距的最小二乘法估计分别为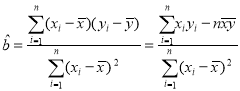 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为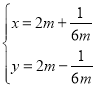 (m为参数),以坐标点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ+
(m为参数),以坐标点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ+![]() )=1.
)=1.
(1)求直线l的直角坐标方程和曲线C的普通方程;
(2)已知点M (2,0),若直线l与曲线C相交于P、Q两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com