【题目】已知数列{an}满足an=logn+1（n+2）（n∈N*）定义使a1a2…ak为整数的数k叫做企盼数，则区间[1，2019]内所有的企盼数的和是______．
【答案】2026
【解析】
根据题意，先求出a1a2…ak可得a1a2a3…ak=log2（k+2），即转化为k+2必须是2的n次幂（n∈N*），即k=2n-2，由k∈[1，2019]可得1≤2n-2≤2019，可求解对应
值，再分项求解即可
∵an=logn+1（n+2）=
（n∈N*），
∴a1a2a3…ak=
…
=log2（k+2），
又a1a2a3…ak为整数，∴k+2必须是2的n次幂（n∈N*），即k=2n-2，
又k∈[1，2019]，∴1≤2n-2≤2019，∴取2≤n≤10，
∴区间[1，2019]内所有的企盼数的和为：
M=（22-2）+（23-2）+（24-2）+…+（210-2）=（22+23+…+210）-2×9=
-18=2026．
故答案为：2026
英才计划同步课时高效训练系列答案科目：高中数学 来源： 题型：
【题目】已知三点A(a，0)，B(0，b)，C(2，2)，其中a>0，b>0.
(1)若O是坐标原点，且四边形OACB是平行四边形，试求a，b的值.
(2)若A，B，C三点共线，试求a+b的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆
.
（1）若圆
的切线在
轴、
轴上的截距相等，求切线方程；
（2）从圆外一点
向该圆引一条切线，切点为
，且有
（
为坐标原点），求使
取得最小值时点
的坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）＝cosx（acosx﹣sinx）
（a∈R），且f （
）
.
（1）求a的值；
（2）求f（x）的单调递增区间；
（3）求f（x）在区间[0，
]上的最小值及对应的x的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，设
是平面内相交成
角的两条数轴 ，
分别是
轴，
轴正方向同向的单位向量，若向量
，则把有序数对
叫做向量
在坐标系
中的坐标，假设
.
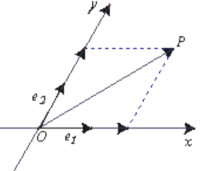
（1）计算
的大小；
（2）设向量
，若
与共线，求实数
的值；
（3）是否存在实数
，使得与向量
垂直，若存在求出的值，若不存在请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
分别是双曲线
的左、右焦点，过点
作垂直与
轴的直线交双曲线于
，
两点，若
为锐角三角形，则双曲线的离心率的取值范围是_______．
【答案】
【解析】
根据双曲线的通径求得点的坐标，将三角形
为锐角三角形，转化为
，即
，将表达式转化为含有离心率的不等式，解不等式求得离心率的取值范围.
根据双曲线的通径可知
，由于三角形为锐角三角形，结合双曲线的对称性可知，故，即
，即
，解得
，故离心率的取值范围是
.
【点睛】
本小题主要考查双曲线的离心率的取值范围的求法，考查双曲线的通径，考查双曲线的对称性，考查化归与转化的数学思想方法，属于中档题.本小题的主要突破口在将三角形为锐角三角形，转化为，利用
列不等式，再将不等式转化为只含离心率的表达式，解不等式求得双曲线离心率的取值范围.
【题型】填空题
【结束】
17
【题目】已知命题
：方程
有两个不相等的实数根；命题
：不等式
的解集为
.若或为真，为假，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】梯形
顶点
在以
为直径的圆上，
米.
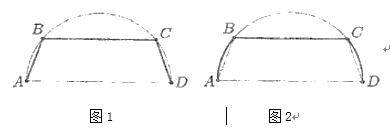
（1）如图1，若电热丝由
这三部分组成，在
上每米可辐射1单位热量，在
上每米可辐射2单位热量，请设计的长度，使得电热丝的总热量最大，并求总热量的最大值；
（2）如图2，若电热丝由弧
和弦这三部分组成，在弧上每米可辐射1单位热量，在弦上每米可辐射2单位热量，请设计的长度，使得电热丝辐射的总热量最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
