
【题目】已知函数![]() .
.
(1)若![]() 在定义域上为单调递减函数,求实数
在定义域上为单调递减函数,求实数![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使得
,使得![]() 恒成立且
恒成立且![]() 有唯一零点,若存在,求出满足
有唯一零点,若存在,求出满足![]() ,
, ![]() 的
的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由![]() 在定义域上单调递减,则
在定义域上单调递减,则![]() 恒成立,求
恒成立,求![]() 的最大值小于等于0即可.
的最大值小于等于0即可.
(2) 当![]() 时,
时, ![]() ,∴
,∴![]() 恒成立,当
恒成立,当![]() 时,由(1)知,
时,由(1)知, ![]() 在
在![]() 内单调递减,分
内单调递减,分![]() ,
, ![]() 两种情况讨论函数的单调性和零点.
两种情况讨论函数的单调性和零点.
试题解析:(1)由已知,函数![]() 的定义域为
的定义域为![]() ,
, ![]()
由![]() 在定义域上单调递减,则
在定义域上单调递减,则![]() 恒成立,
恒成立,
![]() ,所以
,所以![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 单调递增,当
单调递增,当![]() 时,
时, ![]() ,
, ![]() 单调递减.即
单调递减.即![]() 在
在![]() 内单调递增,
内单调递增, ![]() 内单调递减,
内单调递减,
所以![]() .
.
(2)当![]() 时,
时, ![]() ,∴
,∴![]() 恒成立,
恒成立,
当![]() 时,由(1)知,
时,由(1)知, ![]() 在
在![]() 内单调递减,
内单调递减,
(i)若![]() ,
,
由(1)知, ![]() 在
在![]() 内单调递减,
内单调递减,
则![]() ,
, ![]() 无零点,不符合题意;
无零点,不符合题意;
(ii)若![]() ,
,
设![]() ,
, ![]() ,
,
所以![]() ,又
,又![]() ,
,
所以存在![]() ,使得
,使得![]() ,即
,即![]() ,①
,①
且当故当![]() 时,有
时,有![]() ,当
,当![]() 时,有
时,有![]() ,
,
则![]() 在
在![]() 内单调递增,
内单调递增, ![]() 内单调递减,
内单调递减,
由于![]() 恒成立,且
恒成立,且![]() 有唯一零点,∴
有唯一零点,∴![]() .②
.②
结合①,②知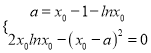 ,③
,③
联立得![]()
设![]() ,则
,则![]() ,
, ![]() ,
,
且当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上有唯一零点
上有唯一零点![]() .
.
即满足方程组③的![]() 唯一,且
唯一,且![]() .
.
设![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,
即满足方程组③的![]() ,所以
,所以![]() .
.
综上所述,存在![]() 即
即![]() ,使得
,使得![]() 恒成立且
恒成立且![]() 有唯一零点.
有唯一零点.


科目:高中数学 来源: 题型:
【题目】(1)由数字1、2、3、4、5、6、7组成无重复数字的七位数
求三个偶数必相邻的七位数的个数及三个偶数互不相邻的七位数的个数
(2)六本不同的书,分为三组,求在下列条件下各有多少种不同的分配方法?
(I)每组两本
(II)一组一本,一组二本,一组三本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 和点
和点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且与圆
且与圆![]() 相切,圆心
相切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]()
(1)求曲线![]() 的方程;
的方程;
(2)点![]() 是曲线
是曲线![]() 与
与![]() 轴正半轴的交点,点
轴正半轴的交点,点![]() 在曲线
在曲线![]() 上,若直线
上,若直线![]() 的斜率
的斜率![]() 满足
满足![]() 求
求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取![]() 名学生的成绩进行统计,作出的茎叶图如下图,记成绩不低于
名学生的成绩进行统计,作出的茎叶图如下图,记成绩不低于![]() 分者为“成绩优良”.
分者为“成绩优良”.

(1)分别计算甲、乙两班![]() 个样本中,化学分数前十的平均分,并据此判断哪种教学方式的教学效果更
个样本中,化学分数前十的平均分,并据此判断哪种教学方式的教学效果更
佳;
(2)甲、乙两班![]() 个样本中,成绩在
个样本中,成绩在![]() 分以下(不含
分以下(不含![]() 分)的学生中任意选取
分)的学生中任意选取![]() 人,求这
人,求这![]() 人来自不同班级的概率;
人来自不同班级的概率;
(3)由以上统计数据填写下面![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为“成绩优良与教学方式有关”?
的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
附: 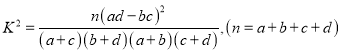
独立性检验临界值表:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时, ![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴左侧的图象,如图所示,并根据图象:
轴左侧的图象,如图所示,并根据图象:
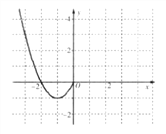
(1)直接写出函数![]() ,
, ![]() 的增区间;
的增区间;
(2)写出函数![]() ,
, ![]() 的解析式;
的解析式;
(3)若函数![]() ,
, ![]() ,求函数
,求函数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:y=3x+3,求:
(1)点P(4,5)关于直线l的对称点坐标;
(2)直线l1:y=x-2关于直线l的对称直线的方程;
(3)直线l关于点A(3,2)的对称直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃.下面叙述不正确的是 ( )
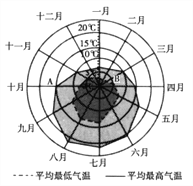
A. 各月的平均最低气温都在0℃以上
B. 七月的平均温差比一月的平均温差大
C. 三月和十一月的平均最高气温基本相同
D. 平均最高气温高于20℃的月份有5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)某班主任对全班50名学生学习积极性和参加社团活动情况进行调查,统计数据如表1所示
表1
参加社团活动 | 不参加社团活动 | 合计 | |
学习积极性高 | 17 | 8 | 25 |
学习积极性一般 | 5 | 20 | 25 |
合计 | 22 | 28 | 50 |
(1)如果随机从该班抽查一名学生,抽到参加社团活动的学生的概率是多少?抽到不参加社团活动且学习积极性一般的学生的概率是多少?
(2)运用独立检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
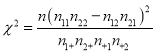
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com