
【题目】如图,在三棱锥![]() 中,
中,![]() 平面ABC,平面
平面ABC,平面![]() 平面PBC,
平面PBC,![]() ,
,![]() .
.
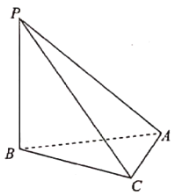
(1)证明:![]() 平面PBC;
平面PBC;
(2)求点C到平面PBA的距离.
科目:高中数学 来源: 题型:
【题目】区块链技术被认为是继蒸汽机、电力、互联网之后,下一代颠覆性的核心技术区块链作为构造信任的机器,将可能彻底改变整个人类社会价值传递的方式,2015年至2019年五年期间,中国的区块链企业数量逐年增长,居世界前列现收集我国近5年区块链企业总数量相关数据,如表
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号 | 1 | 2 | 3 | 4 | 5 |
企业总数量y(单位:千个) | 2.156 | 3.727 | 8.305 | 24.279 | 36.224 |
注:参考数据![]() (其中z=lny).
(其中z=lny).
附:样本(xi,yi)(i=1,2,…,n)的最小二乘法估计公式为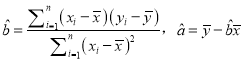
(1)根据表中数据判断,y=a+bx与y=cedx(其中e=2.71828…,为自然对数的底数),哪一个回归方程类型适宜预测未来几年我国区块链企业总数量?(给出结果即可,不必说明理由)
(2)根据(1)的结果,求y关于x的回归方程(结果精确到小数点后第三位);
(3)为了促进公司间的合作与发展,区块链联合总部决定进行一次信息化技术比赛,邀请甲、乙、丙三家区块链公司参赛比赛规则如下:①每场比赛有两个公司参加,并决出胜负;②每场比赛获胜的公司与未参加此场比赛的公司进行下一场的比赛;③在比赛中,若有一个公司首先获胜两场,则本次比赛结束,该公司就获得此次信息化比赛的“优胜公司”,已知在每场比赛中,甲胜乙的概率为![]() ,甲胜丙的概率为
,甲胜丙的概率为![]() ,乙胜丙的概率为
,乙胜丙的概率为![]() ,请通过计算说明,哪两个公司进行首场比赛时,甲公司获得“优胜公司”的概率最大?
,请通过计算说明,哪两个公司进行首场比赛时,甲公司获得“优胜公司”的概率最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且点
,且点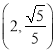 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,在直线
两点,在直线![]() 上存在点
上存在点![]() ,使三角形
,使三角形![]() 为正三角形,求
为正三角形,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上任意一点到其两个焦点
上任意一点到其两个焦点![]() ,
,![]() 的距离之和等于
的距离之和等于![]() ,且圆
,且圆![]() 经过椭圆的焦点.
经过椭圆的焦点.
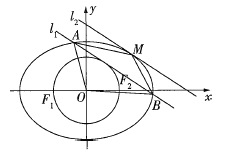
(1)求椭圆的方程;
(2)如图,若直线![]() 与圆O相切,且与椭圆相交于A,B两点,直线
与圆O相切,且与椭圆相交于A,B两点,直线![]() 与
与![]() 平行且与椭圆相切于点M(O,M位于直线
平行且与椭圆相切于点M(O,M位于直线![]() 的两侧).记
的两侧).记![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列{an}中,已知a1+a3=12,a2+a4=18,n∈N*.
(1)求数列{an}的通项公式;
(2)求a3+a6+a9+…+a3n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,有下列4个命题:
,有下列4个命题:
①若![]() ,则
,则![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
②![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
③若![]() 为偶函数,且
为偶函数,且![]() ,则
,则![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
④若![]() 为奇函数,且
为奇函数,且![]() ,则
,则![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
其中正确的命题为 .(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市208年抽样100户居民的月均用电量(单位:千瓦时),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到如下频率分布表:
分组,得到如下频率分布表:
分组 | 频数 | 频率 |
|
| 0.04 |
| 19 |
|
|
| 0.22 |
| 25 | 0.25 |
| 15 | 0.15 |
| 10 |
|
| 5 | 0.05 |
(1)求表中![]() 的值,并估计2018年该市居民月均用电量的中位数
的值,并估计2018年该市居民月均用电量的中位数![]() ;
;
(2)该城市最近十年的居民月均用电量逐年上升,以当年居民月均用电量的中位数![]() (单位:千瓦时)作为统计数据,下图是部分数据的折线图.
(单位:千瓦时)作为统计数据,下图是部分数据的折线图.
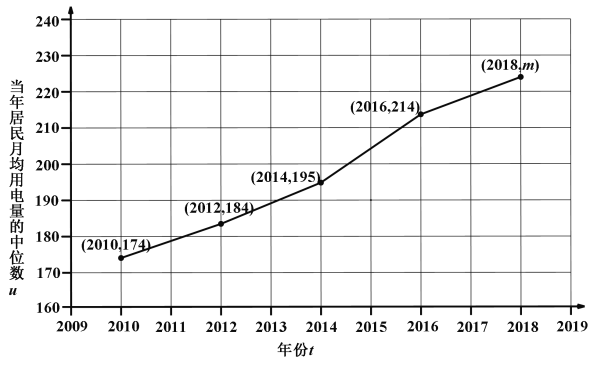
由折线图看出,可用线性回归模型拟合![]() 与年份
与年份![]() 的关系.
的关系.
①为简化运算,对以上数据进行预处理,令![]() ,
,![]() ,请你在答题卡上完成数据预处理表;
,请你在答题卡上完成数据预处理表;
②建立![]() 关于
关于![]() 的线性回归方程,预测2020年该市居民月均用电量的中位数.
的线性回归方程,预测2020年该市居民月均用电量的中位数.
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: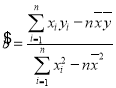 ,
,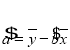 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年第十三届女排世界杯共12支参赛球队,比赛赛制釆取单循环方式,即每支球队进行11场比赛,最后靠积分选出最后冠军.积分规则如下(比赛采取5局3胜制):比赛中以3—0或3—1取胜的球队积3分,负队积0分;而在比赛中以3—2取胜的球队积2分,负队积1分.9轮过后,积分榜上的前2名分别为中国队和美国队,中国队积26分,美国队积22分.第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为![]() .
.
(1)第10轮比赛中,记中国队3—1取胜的概率为![]() ,求
,求![]() 的最大值点
的最大值点![]() .
.
(2)以(1)中的![]() 作为
作为![]() 的值.
的值.
(i)在第10轮比赛中,中国队所得积分为![]() ,求
,求![]() 的分布列;
的分布列;
(ⅱ)已知第10轮美国队积3分,判断中国队能否提前一轮夺得冠军(第10轮过后,无论最后一轮即第11轮结果如何,中国队积分最多)?若能,求出相应的概率;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com