
| A. | (-2018,-2016) | B. | (-∞,-2016) | C. | (-2019,-2016) | D. | (-∞,-2019) |
分析 先构造函数g(x)=x3f(x),再根据导数和函数的单调性的关系得到g(x)在(-∞,0)为增函数,由(x+2016)3f(x+2016)+274f(-3)>0得到g(x+2016)>g(-3)根据函数的单调性即可求出答案.
解答 解:令g(x)=x3f(x),
∴g′(x)=3x2f(x)+x3f′(x),
∵3f(x)+x2f′(x)<0,
x<0时,g′(x)>0,
∴g(x)在(-∞,0)为增函数,
∵(x+2016)3f(x+2016)+27f(-3)>0,
∴(x+2016)3f(x+2016)>(-3)3f(-3),
即g(x+2016)>g(-3),
∴$\left\{\begin{array}{l}{x+2016<0}\\{x+2016>-3}\end{array}\right.$,
解得:-2019<x<-2016,
故选:C.
点评 本题考查函数的单调性与导数的关系,两个函数乘积的导数的求法,而构造函数是解本题的关键.


科目:高中数学 来源: 题型:选择题
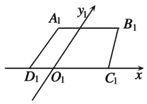 如图,梯形A1B1C1D1是一平面图形ABCD的直观图(斜二测),若AD∥Oy,AB∥CD,A1B1=$\frac{3}{4}{C_1}{D_1}=3,{A_1}{D_1}$=1,则原平面图形ABCD的面积是( )
如图,梯形A1B1C1D1是一平面图形ABCD的直观图(斜二测),若AD∥Oy,AB∥CD,A1B1=$\frac{3}{4}{C_1}{D_1}=3,{A_1}{D_1}$=1,则原平面图形ABCD的面积是( )| A. | 14. | B. | 7 | C. | $14\sqrt{2}$ | D. | $7\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
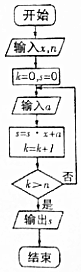 如图是实现秦九韶算法的程序框图,若输入的x=2,n=2,依次输入a=3,4,5,6,7,…,则输出的s=( )
如图是实现秦九韶算法的程序框图,若输入的x=2,n=2,依次输入a=3,4,5,6,7,…,则输出的s=( )| A. | 3 | B. | 10 | C. | 25 | D. | 56 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 制作模型数x(个) | 10 | 20 | 30 | 40 | 50 |
| 花费时间y(分钟) | 64 | 69 | 75 | 82 | 90 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com