
【题目】采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随即编号为1,2…960,分组后在第一组采用简单随机抽样的方法抽到的号码为5,抽到的32人中,编号落入区间[1,450]的人做问卷A,编号落入区间[451,750]的人做问卷B,其余的人做问卷C,则抽到的32人中,做问卷C的人数为( )
A.15
B.10
C.9
D.7
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+(2b﹣1)x+6b﹣a为偶函数,且f(x+1)﹣f(x)=2x+1.
(1)求函数f(x)的解析式;
(2)设g(x)=f(x)+λx,求函数g(x)在[0,1]内的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项为正数的数列{an}的前n项和为Sn , 且满足:Sn= ![]() an2+
an2+ ![]() an+
an+ ![]() (n∈N*)
(n∈N*)
(1)求an
(2)设数列{ ![]() }的前n项和为Tn , 证明:对一切正整数n,都有Tn<
}的前n项和为Tn , 证明:对一切正整数n,都有Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点. 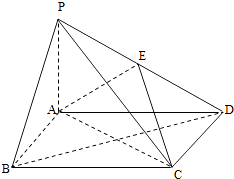
(1)证明:PB∥平面AEC;
(2)设AP=1,AD= ![]() ,三棱锥P﹣ABD的体积V=
,三棱锥P﹣ABD的体积V= ![]() ,求A到平面PBC的距离.
,求A到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为坐标原点,点
为坐标原点,点![]() 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且
,且![]() .
.
(1)求椭圆的标准方程;
(2)圆![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与圆
与圆![]() 相切,并与椭圆交于不同的两点
相切,并与椭圆交于不同的两点![]() ,
,![]() ,当
,当![]() ,且满足
,且满足![]() 时,求
时,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)若![]() 存在极小值
存在极小值![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,如果存在两个不相等的正数
时,如果存在两个不相等的正数![]() ,使得
,使得![]() ,求证:
,求证:![]() .
.
请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,甲向如图1所示的平面区域内随机掷点、乙向如图2所示的平面区域内随机掷点,假设点落在区域内任意一点的可能性相同.已知图1中小圆的半径是大圆半径的二分之一,图2中小正方形的顶点为大正方形各边的中点.
(1)甲、乙各掷点一次,求至少有一人掷点落在阴影区域的概率;
(2)甲、乙各掷点两次,记点落在阴影区域的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.

图1图2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ).以原点
).以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,与直角坐标系
轴正半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围;
的取值范围;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com