
【题目】△ABC中,角A,B,C的对边分别为a,b,c,且三角形的面积S= ![]() accosB.
accosB.
(1)求角B的大小;
(2)若a=2 ![]() ,点D在AB的延长线上,且AD=3,cos∠ADC=
,点D在AB的延长线上,且AD=3,cos∠ADC= ![]() ,求b的值.
,求b的值.
【答案】
(1)解:∵S= ![]() accosB=
accosB= ![]() acsinB,
acsinB,
∴tanB= ![]() ,
,
∴B= ![]() .
.
(2)解:如图,
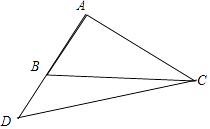
∵B= ![]() .∴∠CBD=
.∴∠CBD= ![]() ,
,
∵cos∠ADC= ![]() ,∴sin∠ADC=
,∴sin∠ADC= ![]() =
= ![]() ,
,
∴在△BCD中,由正弦定理 ![]() ,可得:
,可得: ![]() ,解得:CD=9,
,解得:CD=9,
∴在△ADC中,由余弦定理可得:b2=AD2+CD2﹣2ADCDcos∠ADC=9+81﹣2× ![]() =54.
=54.
∴b=3 ![]() .
.
【解析】(1)由已知利用三角形面积公式,同角三角函数基本关系式可求tanB= ![]() ,由特殊角的三角函数值即可得解B的值.(2)由已知可求∠CBD=
,由特殊角的三角函数值即可得解B的值.(2)由已知可求∠CBD= ![]() ,sin∠ADC=
,sin∠ADC= ![]() ,由正弦定理解得CD,进而在△ADC中,由余弦定理可得b的值.
,由正弦定理解得CD,进而在△ADC中,由余弦定理可得b的值.
【考点精析】根据题目的已知条件,利用正弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,过椭圆 ![]() 右焦点的直线
右焦点的直线 ![]() 交椭圆C于M,N两点,P为M,N的中点,且直线OP的斜率为
交椭圆C于M,N两点,P为M,N的中点,且直线OP的斜率为 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设另一直线l与椭圆C交于A,B两点,原点O到直线l的距离为 ![]() ,求△AOB面积的最大值.
,求△AOB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆C1: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,x轴被曲线C2:y=x2﹣b截得的线段长等于C1的长半轴长.
,x轴被曲线C2:y=x2﹣b截得的线段长等于C1的长半轴长. 
(Ⅰ)求C1 , C2的方程;
(Ⅱ)设C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA,MB分别与C1相交于D,E.
(i)证明:MD⊥ME;
(ii)记△MAB,△MDE的面积分别是S1 , S2 . 问:是否存在直线l,使得 ![]() =
= ![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在海岸![]() 处发现北偏东
处发现北偏东![]() 方向,距
方向,距![]() 处
处![]() 海里的
海里的![]() 处有一艘走私船.在
处有一艘走私船.在![]() 处北偏西
处北偏西![]() 方向,距
方向,距![]() 处
处![]() 海里的
海里的![]() 处的我方缉私船奉命以
处的我方缉私船奉命以![]() 海里
海里![]() 小时的速度追截走私船,此时走私船正以
小时的速度追截走私船,此时走私船正以![]() 海里
海里![]() 小时的速度从
小时的速度从![]() 处向北偏东
处向北偏东![]() 方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴的非负半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acosθ(a>0),l: 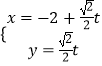 (t为参数)
(t为参数)
(1)求曲线C的普通方程,l的直角坐标方程
(2)设l与C交于M,N两点,点P(﹣2,0),若|PM|,|MN|,|PN|成等比数列,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉三角,是二项式系数在三角形中的一种几何排列。在欧洲,这个表叫做帕斯卡三角形。帕斯卡(1623——1662)是在1654年发现这一规律的,比杨辉要迟![]() 年,比贾宪迟
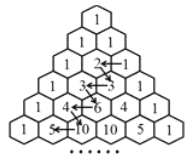
年,比贾宪迟![]() 年。如图的表在我国南宋数学家杨辉1261年所著的《详解九章算法》一书里就出现了,这又是我国数学史上的一个伟大成就。如图所示,在“杨辉三角”中,从1开始箭头所指的数组成一个锯齿形数列:
年。如图的表在我国南宋数学家杨辉1261年所著的《详解九章算法》一书里就出现了,这又是我国数学史上的一个伟大成就。如图所示,在“杨辉三角”中,从1开始箭头所指的数组成一个锯齿形数列:![]() ,则此数列前
,则此数列前![]() 项和为________.
项和为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2c﹣a)cosB﹣bcosA=0.
(Ⅰ)求角B的大小;
(Ⅱ)求 ![]() sinA+sin(C﹣
sinA+sin(C﹣ ![]() )的取值范围.
)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知曲线C1的参数方程为 ![]() ,(α为参数,且α∈[0,π]),曲线C2的极坐标方程为ρ=﹣2sinθ.
,(α为参数,且α∈[0,π]),曲线C2的极坐标方程为ρ=﹣2sinθ.
(Ⅰ)求C1的极坐标方程与C2的直角坐标方程;
(Ⅱ)若P是C1上任意一点,过点P的直线l交C2于点M,N,求|PM||PN|的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com