练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在等比数列中，前n项和为Sn，已知S4=2，S8=8，求S12.

    思路解析：若把给定条件都用a1，q表示，通过解方程组可以求得，这是基本方法.但注意到S4，S8，S12是有规律的，可以考虑用等比数列的性质来解.

    解法一：设等比数列的公比为q，

    若q=1，则S4=4a1=2，∴a1=.

    S8=8a1=8，a1=1.

    这是相互矛盾的，因此q≠1.

    ∴S4=，S8= .

    1+q4=4.

    ∴q4=3.

    而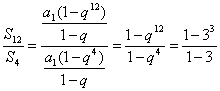=13.

    ∴S12=26.

    解法二：在等比数列中，S4，S8-S4，S12-S8仍然成等比数列，即2，6，S12-8成等比数列.

    ∴2（S12-8）=62.

    解得S12=26.

    深化升华

    （1）应用等比数列的前n项和公式一定要先验证公比q是否可以是1，然后再选择公式.

    （2）由Sn=（1-qn）可以看出，是常数，Sn仅随qn变化.因此，在解法一中，不必求出的值，只需通过S4，S8的比值来求得q，然后求得S12.

    （3）在等比数列中，Sn，S2n-Sn，S3n-S2n仍成等比数列，其公比为qn.

    在应用此性质时，注意不是Sn，S2n，S3n成等比数列.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014届湖北省荆门市高一下学期期末质量检测数学试卷（解析版） 题型：填空题

    在等比数列中，前n项和为,若，则公比的值为           .

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年甘肃省高三上学期第三次月考数学文卷 题型：选择题

    在等比数列中，前n项和为，若，，则公比的值是   （    ）

    A、2          B、-2            C、3         D、-3

     

    查看答案和解析>>

    科目：高中数学 来源：2011届甘肃省天水一中高三上学期第三次月考数学文卷 题型：单选题

    在等比数列中，前n项和为，若，，则公比的值是  （   ）

    A．2B．-2 C．3D．-3

    查看答案和解析>>

    科目：高中数学 来源：甘肃省天水一中2011届度高三第一学期第三阶段考试数学文 题型：选择题

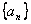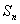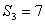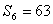     在等比数列中，前n项和为，若，，则公比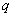的值是    （    ）

        A．2            B．-2               C．3            D．-3

     

    查看答案和解析>>

    同步练习册答案