
分析 根据三维形式的柯西不等式便可得到$[(\sqrt{a+1})^{2}+(\sqrt{b+1})^{2}+(\sqrt{c+1})^{2}][{1}^{2}+{1}^{2}+{1}^{2}]$$≥(\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1})^{2}$,从而便可得到$\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1}≤\sqrt{15}$,并且可知当a=b=c=$\frac{2}{3}$时取“=”,从而便可证出$\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1}<4$.
解答 证明:根据柯西不等式:
$[(\sqrt{a+1})^{2}+(\sqrt{b+1})^{2}+(\sqrt{c+1})^{2}][{1}^{2}+{1}^{2}+{1}^{2}]$$≥(\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1})^{2}$;
左边=3(a+b+c+3)=15;
∴$\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1}≤\sqrt{15}$;
当且仅当$\frac{\sqrt{a+1}}{1}=\frac{\sqrt{b+1}}{1}=\frac{\sqrt{c+1}}{1}$,即a=b=c=$\frac{2}{3}$时取“=”;
∴$\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1}≤\sqrt{15}<\sqrt{16}$;
即$\sqrt{a+1}+\sqrt{b+1}+\sqrt{c+1}<4$.
点评 考查三维形式的柯西不等式公式:$({{a}_{1}}^{2}+{{a}_{2}}^{2}+{{a}_{3}}^{2})({{b}_{1}}^{2}+{{b}_{2}}^{2}+{{b}_{3}}^{2})≥$$({a}_{1}{b}_{1}+{a}_{2}{b}_{2}+{a}_{3}{b}_{3})^{2}$,并且清楚等号成立的条件,放缩法在不等式证明中的应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
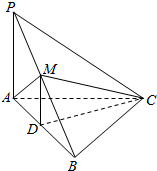 已知三棱锥P-ABC中,PA⊥平面ABC,底面ABC为边长等于3的正三角形,D、M为AB、PB中点,且△PAM为正三角形.
已知三棱锥P-ABC中,PA⊥平面ABC,底面ABC为边长等于3的正三角形,D、M为AB、PB中点,且△PAM为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com