
【题目】设椭圆![]()
![]() 的一个焦点为
的一个焦点为![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,
,![]() 为坐标原点,
为坐标原点,
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆![]() 恒有两个交点
恒有两个交点![]() 、
、![]() ,且
,且![]() ?若存在,写出该圆的方程,并求
?若存在,写出该圆的方程,并求![]() 的最大值,若不存在说明理由.
的最大值,若不存在说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为:
的极坐标方程为:![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出曲线![]() 的极坐标方程,并指出它是何种曲线;
的极坐标方程,并指出它是何种曲线;
(Ⅱ)设![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十二生肖,又称十二属相,中国古人拿十二种动物来配十二地支,组成子鼠、丑牛、寅虎、卯兔、辰龙、巳蛇、午马、未羊、申猴、酉鸡、戌狗、亥猪十二属相。现有十二生肖吉祥物各一件,甲、乙、丙三位同学一次随机抽取一件作为礼物,甲同学喜欢马、牛,乙同学喜欢马、龙、狗,丙同学除了鼠不喜欢外其他的都喜欢,则这三位同学抽取的礼物都喜欢的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值.求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD与△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
①![]() ;
;
②∠BAC=60°;
③三棱锥D﹣ABC是正三棱锥;
④平面ADC的法向量和平面ABC的法向量互相垂直.
其中正确结论的序号是 .(请把正确结论的序号都填上)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业者计划在某旅游景区附近租赁一套农房发展成特色“农家乐”,为了确定未来发展方向此创业者对该景区附近五家“农家乐”跟踪调查了100天,这五家“农家乐的收费标准互不相同得到的统计数据如下表,x为收费标准(单位:元/日),t为入住天数(单位:天),以频率作为各自的“入住率”,收费标准x与“入住率”y的散点图如图
x | 100 | 150 | 200 | 300 | 450 |
t | 90 | 65 | 45 | 30 | 20 |
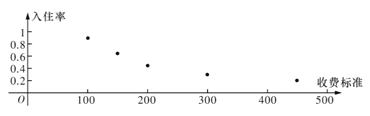
(1)若从以上五家“农家乐”中随机抽取两家深人调查,记![]() 为“入住率超过0.6的农家乐的个数,求
为“入住率超过0.6的农家乐的个数,求![]() 的概率分布列
的概率分布列
(2)z=lnx,由散点图判断![]() 与
与![]() 哪个更合适于此模型(给出判断即可不必说明理由)?并根据你的判断结果求回归方程(a,
哪个更合适于此模型(给出判断即可不必说明理由)?并根据你的判断结果求回归方程(a,![]() 的结果精确到0.1)
的结果精确到0.1)
(3)根据第(2)问所求的回归方程,试估计收费标准为多少时,100天销售额L最大?(100天销售额L=100×入住率×收费标准x)
参考数据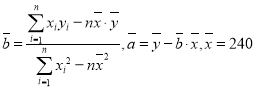 ,
,![]() ,
,![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com