(本小题满分14分)已知数列

满足

某同学欲求

的通项公式,他想,如能找到一个函数

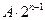



,把递推关系变成


后,就容易求出

的通项了.
(Ⅰ)请问:他设想的

存在吗?

的通项公式是什么?
(Ⅱ)记

,若不等式
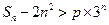
对任意

都成立,求实数

的取值范围.
(Ⅰ)
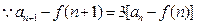
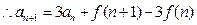
,
所以只需

………………2分
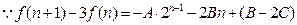
,
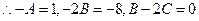
………………3分
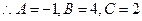
.故他设想的

存在,且

………………4分
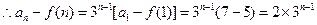
………………5分

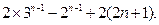
………………6分
(Ⅱ)
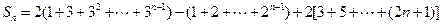
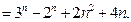

………………7分
由
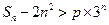
,得
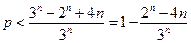
.………………8分
设

,
则


………………9分
当
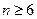
时,
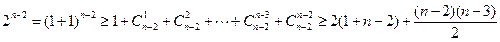

,(用数学归纳法证也行)………………11分

时,

. 容易验证 ,
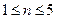
时,
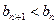
,
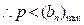

………………13分

的取值范围为

. ………………14分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分8分)
数列
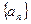
满足
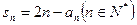
。
(Ⅰ)计算
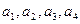
,并由此猜想通项公式
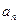
;
(Ⅱ)用数学归纳法证明(Ⅰ)中的猜想。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知数列
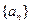
满足
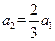
,
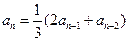
(
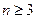
且
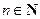
)
(Ⅰ)证明数列
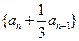
是常数列;
(Ⅱ)求数列
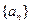
的通项公式;
(Ⅲ)当
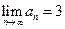
时,求数列
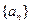
的前
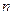
项和.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题12分)已知等比数列
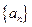
中,
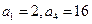
。
(1)求数列
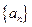
的通项公式;
(2)设等差数列
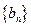
中,
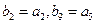
,求数列
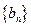
的前
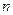
项和
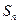
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设数列

(1)求数列

的通项公式;
(2)设

,求数列

(3)设

,

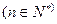
,记

,设数列

的前

项和为

,求证:对任意正整数

都有

;
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设等差数列
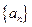

的前
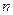
项和为
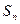
,等比数列
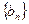
的前
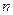
项和为
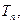
已知数列
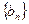
的公比

为
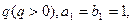
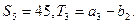
(Ⅰ

)求数列
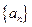
,
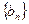
的通项公式;
(Ⅱ)求
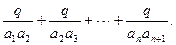

查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
设等比数列
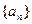
的公比为q,前n项和为S
n,若S
n+1,S
n,S
n+2成等差数列,则q
的值为
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
记等差数列

的前

项和

,利用倒序求和的方法得:

;类似的,记等比数列

的前

项的积为

,且


,试类比等差数列求和的方法,可将

表示成首项
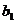
,末项

与项数

的一个关系式,即公式

_______________。
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知数列

满足

,且对任意的正整数

都有

,若数列

的前
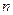
项和为

,则

=
查看答案和解析>>

 满足
满足
 的通项公式,他想,如能找到一个函数
的通项公式,他想,如能找到一个函数
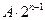


 ,把递推关系变成
,把递推关系变成
 后,就容易求出
后,就容易求出 的通项了.
的通项了. 存在吗?
存在吗? 的通项公式是什么?
的通项公式是什么? ,若不等式
,若不等式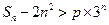 对任意
对任意 都成立,求实数
都成立,求实数 的取值范围.
的取值范围. 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案 的前
的前 项和
项和 ,利用倒序求和的方法得:
,利用倒序求和的方法得: ;类似的,记等比数列
;类似的,记等比数列 的前
的前 项的积为
项的积为 ,且
,且
 ,试类比等差数列求和的方法,可将
,试类比等差数列求和的方法,可将 表示成首项
表示成首项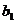 ,末项
,末项 与项数
与项数 的一个关系式,即公式
的一个关系式,即公式 _______________。
_______________。