
分析 (1)讨论去绝对值号函数f(x)=,从而分别求最小值,再利用分段函数求最小值;
(2)讨论去绝对值号函数f(x),再根据二次函数的单调性及分段函数的单调性从而求函数的最小值,再令最小值大于3,从而求实数a的取值范围
解答 解:(1)当a=1时,f(x)=x2+1+|x+1|=$\left\{\begin{array}{l}{{x}^{2}+x+2,x≥-1}\\{{x}^{2}-x,x<-1}\end{array}\right.$,
当x≥-1时,f(x)=x2+x+2=(x+$\frac{1}{2}$)2+$\frac{7}{4}$≥$\frac{7}{4}$,
当x<-1时,f(x)=x2-x=(x-$\frac{1}{2}$)2-$\frac{1}{4}$<f(-1)=1+1=2,
∴当a=1时,函数f(x)的最小值为$\frac{7}{4}$,
(2)当x≥-a时,f(x)=x2+x+a2+a=(x+$\frac{1}{2}$)2+a2+a-$\frac{1}{4}$,
当x<-a时,f(x)=x2-x=(x-$\frac{1}{2}$)2-$\frac{1}{4}$,
当-a≤-$\frac{1}{2}$时,即a≥$\frac{1}{2}$时,f(x)min=a2+a-$\frac{1}{4}$>3,解得a>$\frac{-1+\sqrt{14}}{2}$,
当-$\frac{1}{2}$<-a<$\frac{1}{2}$时,即-$\frac{1}{2}$<a<$\frac{1}{2}$时,f(x)min=f(-a)=2a2>3,此时无解,
当-a≥$\frac{1}{2}$时,即a≤-$\frac{1}{2}$时,f(x)min=f($\frac{1}{2}$)=-$\frac{1}{4}$<3,此时不存在,
综上所述a的取值范围($\frac{-1+\sqrt{14}}{2}$,+∞)
点评 本题考查了绝对值函数的化简与段函数的最值的求法,同时考查了分类讨论的数学思想应用,属于难题.


科目:高中数学 来源: 题型:解答题
 用部分自然构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aii=i.每行中的其他各数分别等于其“肩膀”上的两个数之和.设第n(n∈N+)行的第二个数为bn(n≥2).
用部分自然构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aii=i.每行中的其他各数分别等于其“肩膀”上的两个数之和.设第n(n∈N+)行的第二个数为bn(n≥2).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
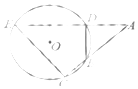 如图,圆O的弦ED,CB的延长线交于点A.若BD⊥AE,AB=4,BC=2,AD=3,则DE= ;CE= .( )
如图,圆O的弦ED,CB的延长线交于点A.若BD⊥AE,AB=4,BC=2,AD=3,则DE= ;CE= .( )| A. | 5、2$\sqrt{7}$ | B. | 5、7$\sqrt{7}$ | C. | 7 7$\sqrt{2}$ | D. | 5、$\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com