
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
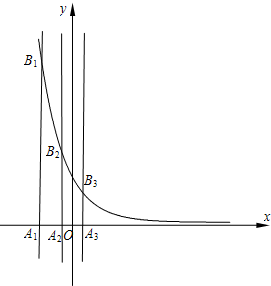 (2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(
(2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省韶关市高三第一次调研测试文科数学试卷(解析版) 题型:解答题
设等差数列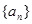 的公差
的公差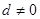 ,等比数列
,等比数列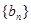 公比为
公比为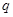 ,且
,且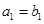 ,
,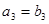 ,
,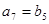
(1)求等比数列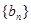 的公比
的公比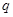 的值;
的值;
(2)将数列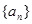 ,
,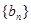 中的公共项按由小到大的顺序排列组成一个新的数列
中的公共项按由小到大的顺序排列组成一个新的数列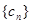 ,是否存在正整数
,是否存在正整数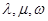 (其中
(其中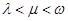 )使得
)使得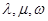 和
和 都构成等差数列?若存在,求出一组
都构成等差数列?若存在,求出一组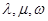 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省韶关市高三第一次调研测试数学理科试卷(解析版) 题型:解答题
设等差数列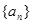 的公差
的公差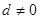 ,等比数列
,等比数列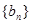 为公比为
为公比为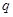 ,且
,且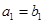 ,
,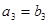 ,
,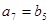 .
.
(1)求等比数列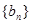 的公比
的公比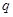 的值;
的值;
(2)将数列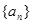 ,
,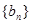 中的公共项按由小到大的顺序排列组成一个新的数列
中的公共项按由小到大的顺序排列组成一个新的数列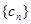 ,是否存在正整数
,是否存在正整数 (其中
(其中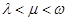 )使得
)使得 和
和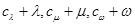 都构成等差数列?若存在,求出一组
都构成等差数列?若存在,求出一组 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com