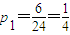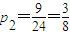【答案】
分析:(1)由题意知本题是一个等可能事件的概率,试验发生所包含的事件数通过分类列举共有24种结果,满足条件的事件列举出共有6种结果,根据等可能事件的概率公式得到结果.
(2)由题意知本题是一个等可能事件的概率,试验发生所包含的事件数通过第一问列举得到共有24种结果,满足条件的事件数也可以通过列举得到,最后求得概率.
解答:解:(1)由题意知本题是一个等可能事件的概率,
试验发生所包含的事件数通过列举得到
A排第一的情况:(A,B,C,D),(A,B,D,C),(A,C,B,D),(A,C,D,B)
(A,D,B,C),(A,D,C,B)
B排第一的情况:(B,A,C,D),(B,A,D,C),(B,C,A,D),(B,C,D,A)
(B,D,A,C),(B,D,C,A)
C排第一的情况:(C,A,B,D),(C,A,D,B),(C,,B,A,D),(C,B,D,A)
(C,D,A,B),(C,D,B,A)
D排第一的情况:(D,A,B,C),(D,A,C,B),(D,B,A,C),(D,B,C,A)
(D,C,A,B),(D,C,B,A)共24种情况
满足条件的事件恰好有两名同学排名不变的是:(A,B,D,C)(A,C,B,D),(A,D,C,B),(D,B,C,A),(C,,B,A,D),(B,A,C,D),共6种情况
所以恰好有两名同学排名不变的概率为
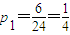
(2)由题意知本题是一个等可能事件的概率,
试验发生所包含的事件数通过第一问列举得到共有24种结果
满足条件的事件是四名同学排名全变的是:(B,A,D,C),(B,C,D,A),(B,D,A,C),
(B,D,C,A),(C,A,D,B),(C,D,A,B),(C,D,B,A),(D,A,B,C),(D,A,C,B)共9种情况
所以四名同学排名全变的概率为
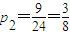 点评:
点评:本题考查等可能事件的概率,本题解题的关键是通过分类列举得到所有的事件数和满足条件的事件数,在列举时要按照一定的规律分类,做到不重不漏,本题是一个基础题.