
【题目】已知函数![]() ,
,![]() ;
;
![]() 若函数
若函数![]() 在
在![]() 上存在零点,求a的取值范围;
上存在零点,求a的取值范围;
![]() 设函数
设函数![]() ,
,![]() ,当
,当![]() 时,若对任意的
时,若对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( )
A.62%B.56%
C.46%D.42%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 过点
过点![]() ,且直线
,且直线![]() 过
过![]() 的左焦点.
的左焦点.
(1)求![]() 的方程;
的方程;
(2)设![]() 为
为![]() 上的任一点,记动点
上的任一点,记动点![]() 的轨迹为
的轨迹为![]() ,
,![]() 与
与![]() 轴的负半轴、
轴的负半轴、![]() 轴的正半轴分别交于点
轴的正半轴分别交于点![]() ,
,![]() 的短轴端点关于直线
的短轴端点关于直线![]() 的对称点分别为
的对称点分别为![]() 、
、![]() ,当点
,当点![]() 在直线
在直线![]() 上运动时,求
上运动时,求![]() 的最小值;
的最小值;
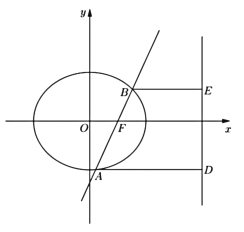
(3)如图,直线![]() 经过
经过![]() 的右焦点
的右焦点![]() ,并交
,并交![]() 于
于![]() 两点,且
两点,且![]() 在直线
在直线![]() 上的射影依次为
上的射影依次为![]() ,当
,当![]() 绕
绕![]() 转动时,直线
转动时,直线![]() 与
与![]() 是否相交于定点?若是,求出定点的坐标,否则,请说明理由.
是否相交于定点?若是,求出定点的坐标,否则,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
文艺节目 | 新闻节目 | 总计 | |
20至40岁 | 30 | 18 | 48 |
大于40岁 | 20 | 32 | 52 |
总计 | 50 | 50 | 100 |
(1)用分层抽样方法在收看文艺节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(2)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为大于40岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有两个不同零点
有两个不同零点![]() 、
、![]() (
(![]() ),设函数
),设函数![]() 的定义域为
的定义域为![]() ,且
,且![]() 的最大值记为
的最大值记为![]() ,最小值记为
,最小值记为![]() .
.
(1)求![]() (用
(用![]() 表示);
表示);
(2)当![]() 时,试问以
时,试问以![]() 、
、![]() 、
、![]() 为长度的线段能否组成一个三角形,如果不一定,进一步求出
为长度的线段能否组成一个三角形,如果不一定,进一步求出![]() 的取值范围,使它们能组成一个三角形;
的取值范围,使它们能组成一个三角形;
(3)求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出了根据我国2012年~2018年水果人均占有量![]() (单位:
(单位:![]() )和年份代码
)和年份代码![]() 绘制的散点图和线性回归方程的残差图(2012年~2018年的年份代码
绘制的散点图和线性回归方程的残差图(2012年~2018年的年份代码![]() 分别为1~7).
分别为1~7).
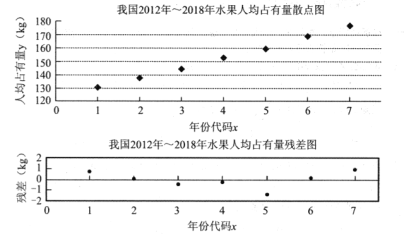
(1)根据散点图分析![]() 与
与![]() 之间的相关关系;
之间的相关关系;
(2)根据散点图相应数据计算得![]() ,求
,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)根据线性回归方程的残差图,分析线性回归方程的拟合效果.(精确到0.01)
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: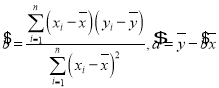 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、![]() 后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( )
后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( )
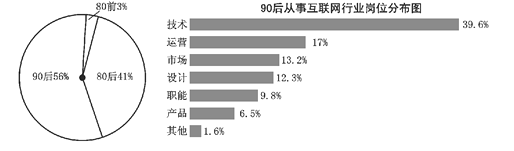
A. 互联网行业从业人员中![]() 后占一半以上
后占一半以上
B. 互联网行业中从事技术岗位的人数超过总人数的![]()
C. 互联网行业中从事运营岗位的人数![]() 后比
后比![]() 前多
前多
D. 互联网行业中从事运营岗位的人数![]() 后比
后比![]() 后多
后多
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com