
用数学归纳法证明不等式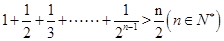 ,第二步由k到k+1时不等式左边需增加( )
,第二步由k到k+1时不等式左边需增加( )
A.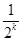 | B.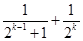 |
C.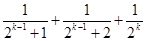 | D.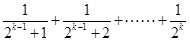 |
科目:高中数学 来源: 题型:单选题
设 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且 满足:“当
满足:“当 成立时,总可推出
成立时,总可推出 成立”,那么,下列命题总成立的是 ( )
成立”,那么,下列命题总成立的是 ( )
A.若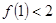 成立,则 成立,则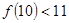 成立 成立 |
B.若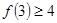 成立,则当 成立,则当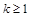 时,均有 时,均有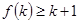 成立 成立 |
C.若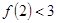 成立,则 成立,则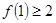 成立 成立 |
D.若 成立,则当 成立,则当 时,均有 时,均有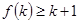 成立 成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线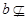 平面
平面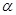 ,直线
,直线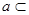 平面
平面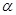 ,直线
,直线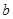 ∥平面
∥平面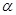 ,则直线
,则直线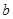 ∥直线
∥直线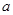 ”的结论显然是错误的,这是因为 ( )
”的结论显然是错误的,这是因为 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用反证法证明命题:“a,b∈N,ab可被5整除,那么a,b中至少有一个能被5整除”时,假设的内容应为( )
| A.a,b都能被5整除 | B.a,b都不能被5整除 |
| C.a,b不都能被5整除 | D.a不能被5整除 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
由“半径为R的圆内接矩形中,正方形的面积最大”,推理出“半径为R的球的内接长方体中,正方体的体积最大”是( )
| A.归纳推理 | B.类比推理 | C.演绎推理 | D.以上都不是 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
如图的三角形数阵中,满足:(1)第1行的数为1;(2)第 (
( )行首尾两数均为
)行首尾两数均为 ,其余的数都等于它肩上的两个数相加,则第
,其余的数都等于它肩上的两个数相加,则第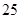 行中第
行中第 个数是____________.
个数是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
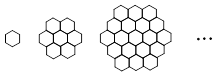
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为
一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,
按此规律,以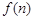 表示第
表示第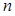 幅图的蜂巢总数.则
幅图的蜂巢总数.则 =_____,
=_____, =___________.
=___________.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用数学归纳法证明“当n为正奇数时,xn+yn能被x+y整除”的第二步
是( ).
| A.假使n=2k+1时正确,再推n=2k+3正确 |
| B.假使n=2k-1时正确,再推n=2k+1正确 |
| C.假使n=k时正确,再推n=k+1正确 |
| D.假使n≤k(k≥1),再推n=k+2时正确(以上k∈N+) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com