
下列四个命题:
① 命题 :
: ;则
;则 命题是;
命题是; ;
;
② (
( 为正整数)的展开式中,
为正整数)的展开式中, 的系数小于90,则
的系数小于90,则 的值为1;
的值为1;
③从总体中抽取的样本 .若记
.若记 ,则回归直线
,则回归直线 必过点
必过点  ;
;
④过双曲线 的右焦点作直线交双曲线于A、B两点,若弦长|AB|=8,则这样的直线恰好有3条;
的右焦点作直线交双曲线于A、B两点,若弦长|AB|=8,则这样的直线恰好有3条;
其中正确的序号是 (把你认为正确的序号都填上).
②③④
【解析】
试题分析:在① 中, 和
和 都不能判定正确与否,所以不是命题;在② 中,
都不能判定正确与否,所以不是命题;在② 中,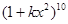 (
( 为正整数)的展开式中,含有
为正整数)的展开式中,含有 的项是
的项是 ,由
,由 且
且 为正整数得,
为正整数得, 的值为1;在③ 中,回归直线
的值为1;在③ 中,回归直线 必过样本点的中心
必过样本点的中心  ;在④ 中,双曲线
;在④ 中,双曲线 的右焦点
的右焦点 ,过这焦点且垂直于x轴的直线
,过这焦点且垂直于x轴的直线 与双曲线有两交点,可求得这两交点的距离是8,另过这焦点的两直线都与双曲线左右支各有一个交点,也符合题意,因而这样的直线恰好有3条。
与双曲线有两交点,可求得这两交点的距离是8,另过这焦点的两直线都与双曲线左右支各有一个交点,也符合题意,因而这样的直线恰好有3条。
考点:命题的定义;二项式定理;回归方程;双曲线的性质。
点评:本题第④点较难判断,这要求大家对双曲线要有比较深入的理解。此小题无须求出三条直线的方程,我们可以这样来求解,由题意可求得直线 符合题意,另外,由于右焦点与左顶点的距离是
符合题意,另外,由于右焦点与左顶点的距离是 (小于8),因而另两条直线都与双曲线左右支各有一个交点。
(小于8),因而另两条直线都与双曲线左右支各有一个交点。


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x+1 |
| 2x-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com