已知函数f(x)=x2,g(x)=|x-a|.
(1)当a=2时,求不等式f(x)>g(x)的解集;
(2)设a>1,函数h(x)=f(x)g(x),求h(x)在x∈[1,2]上的最小值.
解:(1)∵x
2>|x-2|
∴{x|x>1或x<-2}
(2)h(x)=x
2|x-a|x∈[1,2]
当1<a≤2 h(x)=x
2|x-a|≥0 在x=a时,最小值为0
当a>2 h(x)=ax
2-x
3 hˊ(x)=3x(

-x)
令hˊ(x)=0,得x=0,x=

当x∈(-∞,0)时 hˊ(x)<0
当x∈(

,+∞)时 hˊ(x)<0
当x∈(0,

)时 hˊ(x)>0
∴当

≥2,h(x)的最小值为h(1)=0
当1<

<2,h(x)的最小值为h(1)与h(2)中较小者
又h(1)=a-1 h(2)=4a-8
∴当2<a≤

h(x)的最小值为h(2)=4a-8
当

<a<3 h(x)的最小值为h(1)=a-1
∴h(x)=
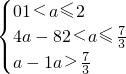
分析:(1)分两种情况去绝对值,再利用一元二次不等式的解法来解.
(2)先有a和x的关系找h(x),再对h(x)用导函数的方法求最值.
点评:带绝对值的函数求最值时,一定要根据绝对值中数的正负来去掉绝对值符号再分段利用单调性解题.

 -x)
-x)
 ,+∞)时 hˊ(x)<0
,+∞)时 hˊ(x)<0 )时 hˊ(x)>0
)时 hˊ(x)>0 ≥2,h(x)的最小值为h(1)=0
≥2,h(x)的最小值为h(1)=0 <2,h(x)的最小值为h(1)与h(2)中较小者
<2,h(x)的最小值为h(1)与h(2)中较小者 h(x)的最小值为h(2)=4a-8
h(x)的最小值为h(2)=4a-8 <a<3 h(x)的最小值为h(1)=a-1
<a<3 h(x)的最小值为h(1)=a-1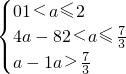


 中考解读考点精练系列答案
中考解读考点精练系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<