
如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 底面
底面![]() ,
,![]()
![]() ,点M在侧棱
,点M在侧棱![]() 上,
上,![]() =60°
=60°
(I)证明:M在侧棱![]() 的中点
的中点
(II)求二面角![]() 的大小。
的大小。
 (I)解法一:作
(I)解法一:作![]() ∥
∥![]() 交
交![]() 于N,作
于N,作![]() 交
交![]() 于E,
于E,
连ME、NB,则![]() 面
面![]() ,
,![]() ,
,![]()
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]()
![]()
![]() 。
。
 在
在![]() 中由
中由![]()
![]()
解得![]() ,从而
,从而![]()
![]() M为侧棱
M为侧棱![]() 的中点M.
的中点M.
解法二:过![]() 作
作![]() 的平行线.
的平行线.
解法三:利用向量处理. 详细可见09年高考参考答案.
(II)分析一:利用三垂线定理求解。在新教材中弱化了三垂线定理。这两年高考中求二面角也基本上不用三垂线定理的方法求作二面角。
过![]() 作
作![]() ∥
∥![]() 交
交![]() 于
于![]() ,作
,作![]() 交
交![]() 于
于![]() ,作
,作![]() 交
交![]() 于
于![]() ,则
,则![]() ∥
∥![]() ,
,![]() 面
面![]() ,面
,面![]()
![]() 面
面![]() ,
,![]() 面
面![]()
![]()
![]() 即为所求二面角的补角.
即为所求二面角的补角.
分析二:利用二面角的定义。在等边三角形![]() 中过点
中过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则点
,则点![]() 为AM的中点,取SA的中点G,连GF,易证
为AM的中点,取SA的中点G,连GF,易证![]() ,则
,则![]() 即为所求二面角.
即为所求二面角.
分析三:利用空间向量求。在两个半平面内分别与交线AM垂直的两个向量的夹角即可。
另外:利用射影面积或利用等体积法求点到面的距离等等,这些方法也能奏效。
总之在目前,立体几何中的两种主要的处理方法:传统方法与向量的方法仍处于各自半壁江山的状况。命题人在这里一定会照顾双方的利益。


科目:高中数学 来源: 题型:
 如图,四棱锥中,底面ABCD是菱形,SA=SD=
如图,四棱锥中,底面ABCD是菱形,SA=SD=| 39 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山西省高三第一次月考摸底理科数学试卷(解析版) 题型:解答题
如图,四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
, ⊥底面
⊥底面 .①证明:平面
.①证明:平面 平面
平面 ;
②若二面角
;
②若二面角 为
为 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省五校联盟模拟考试理科数学试卷 题型:解答题
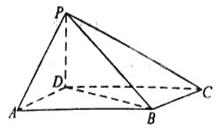
如图,四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, ,
,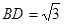 ,
, ⊥底面
⊥底面 .
.
(1)证明:平面 平面
平面 ;
;
(2)若二面角 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。

查看答案和解析>>
科目:高中数学 来源:黑龙江省10-11学年高一下学期期末考试数学(理) 题型:解答题
(本小题满分12分)如图,四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, 底面
底面 .
.
(1)证明: ;
;
(2)若 求二面角
求二面角 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源:2013届山东省济宁市高二3月月考理科数学试卷 题型:解答题
如图,四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, ,
,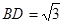 ,
, ⊥底面
⊥底面 .
.
(1)证明:平面 平面
平面 ;
;
(2)若二面角 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com