
【题目】如图,已知四棱锥![]() ,平面
,平面![]() 平面
平面![]() ,四边形
,四边形![]() 是菱形,
是菱形,![]() .
.

(1)若![]() ,证明:
,证明:![]() ;
;
(2)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:高中数学 来源: 题型:
【题目】某车间生产甲、乙两种产品,已知制造一件甲产品需要![]() 种元件5个,
种元件5个,![]() 种元件2个,制造一件乙种产品需要
种元件2个,制造一件乙种产品需要![]() 种元件3个,
种元件3个,![]() 种元件3个,现在只有
种元件3个,现在只有![]() 种元件180个,
种元件180个,![]() 种元件135个,每件甲产品可获利润20元,每件乙产品可获利润15元,试问在这种条件下,应如何安排生产计划才能得到最大利润?
种元件135个,每件甲产品可获利润20元,每件乙产品可获利润15元,试问在这种条件下,应如何安排生产计划才能得到最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 且a≠1,函数
且a≠1,函数![]() .
.
(1)判断并证明f(x)和g(x)的奇偶性;
(2)求g(x)的值域;
(3)若x∈R,都有|f(x)|≥|g(x)|成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究每周累计户外暴露时间是否足够(单位:小时)与近视发病率的关系,对某中学一年级![]() 名学生进行不记名问卷调查,得到如下数据:
名学生进行不记名问卷调查,得到如下数据:

(1)用样本估计总体思想估计该中学一年级学生的近视率;
(2)能否认为在犯错误的概率不超过![]() 的前提下认为不足够的户外暴露时间与近视有关系?
的前提下认为不足够的户外暴露时间与近视有关系?
附: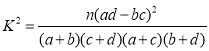 .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教师调查了![]() 名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
男生 | 女生 | 总计 | |
购买数学课外辅导书超过 |
|
|
|
购买数学课外辅导书不超过 |
|
|
|
总计 |
|
|
|
(Ⅰ)根据表格中的数据,是否有![]() 的把握认为购买数学课外辅导书的数量与性别相关;
的把握认为购买数学课外辅导书的数量与性别相关;
(Ⅱ)从购买数学课外辅导书不超过![]() 本的学生中,按照性别分层抽样抽取
本的学生中,按照性别分层抽样抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人询问购买原因,求恰有
人询问购买原因,求恰有![]() 名男生被抽到的概率.
名男生被抽到的概率.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是梯形.BC∥AD,AB=BC=CD=1,AD=2,![]() ,
,![]()
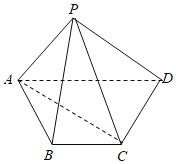
(Ⅰ)证明;AC⊥BP;
(Ⅱ)求直线AD与平面APC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两种理财产品![]() 和
和![]() ,投资这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
,投资这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]() :
:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概率 |
|
|
|
产品![]() :
:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概率 |
|
|
|
注:![]() ,
,![]()
(1)若甲、乙两人分别选择了产品![]() 投资,一年后他们中至少有一人获利的概率大于
投资,一年后他们中至少有一人获利的概率大于![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若丙要将20万元人民币投资其中一种产品,以一年后的投资收益的期望值为决策依据,则丙选择哪种产品投资较为理想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com