
 如图,已知∠DAE=10°,∠CAE=70°,∠DCA=60°,∠DCE=20°,则∠DEA=20°.
如图,已知∠DAE=10°,∠CAE=70°,∠DCA=60°,∠DCE=20°,则∠DEA=20°. 分析 以BC为边向左作等边△BCF,连接EF,以EF为边向下作等边△EFG,连接AG,AF,FD,由已知条件推导出△CDF≌△BDF,△ABF≌△ECA,△AFG≌△DFE,从而能求出∠DEA=∠AEF-∠DEF=50°-30°=20°.
解答 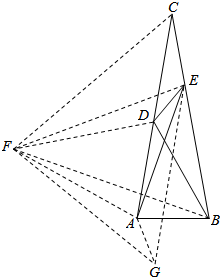 解:以BC为边向左作等边△BCF,连接EF,以EF为边向下作等边△EFG,连接AG,AF,FD,
解:以BC为边向左作等边△BCF,连接EF,以EF为边向下作等边△EFG,连接AG,AF,FD,
则CF=BC=BF,
∠CBF=∠BFC=∠BCF=60°,
EF=EG=FG,
∠EFG=∠FGE=∠FEG=60°,
∵∠DAE=10°,∠EAB=70°,
∴∠BAC=∠DAE+∠EAB=10+70=80°,
∵∠ABC=∠DBA+∠DBE,∠DBA=60°,∠DBC=20°,
∴∠ABC=80°,
∵∠ABC+∠ACB+∠BAC=180°,∴∠ACB=20°,
∠BAC=∠ABC=80°,∴AC=BC,
∠ACB=∠DBC=20°,∴CD=BD,
∵DF=DF,△CDF≌△BDF,
∴∠CFD=∠BFD=$\frac{1}{2}$∠BFC=30°,
∵∠ACF=∠BCF-∠ACB=60°-20°=40°,
AC=CF,
∴∠AFC=∠FAC,
∵∠AFC+∠FAC+∠ACF=180°,∴∠FAC=∠AFC=70°,
∵∠ADF=∠ACF+∠CFD=30°+40°=70°,
∴∠FAC=∠ADF=70°,∴AF=DF,
∵∠ADF+∠FAC+∠AFD=180°,∠AFD=40°,
∵∠AFB=∠AFC-∠BFC=70°-60°=10°,∠AFB=∠DAE=10°,
∵∠ABF=∠ABC-∠CBF=80°-60°=20°,∴∠ABF=∠ACB=20°,
∵BF=AC,∴△ABF≌△ECA,∴AF=AE,∴∠AFE=∠AEF,
∵AG=AG,FG=EG,△AFG≌△AEG,∴∠AGF=∠AGE=$\frac{1}{2}$∠FGE=30°,
∵∠FAE=∠FAC+∠DAE=10°+70°=80°,∠AFE+∠AEF+∠FAE=180°,
∴∠AFE=∠AEF=50°,
∵∠DFE=∠AFE-∠AFD=50°-40°=10°,
∠AFG=∠EFG-∠AFE=60°-50°=10°,
∴∠DFE=∠AFG=10°,
∵EF=FG,AF=DF,
∴△AFG≌△DFE,∴∠AGF=∠DEF,∴∠DEF=30°,
∵∠DEA=∠AEF-∠DEF=50°-30°=20°,
∴∠DEA=20°.
故答案为:20°.
点评 本题考查角的大小的求法,是中档题,解题时要认真审题,注意全等三角形的判定定理和性质定理的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知直角三角形周长为48cm,一锐角交平分线分对边为3:5两部分.
如图,已知直角三角形周长为48cm,一锐角交平分线分对边为3:5两部分.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 三棱锥A-BCD中,△BCD是边长为1的正三角形,点A在平面BCD上的射影为△BCD的中心,E,F分别是BC,BA的中点,EF⊥FD,则三棱锥A-BCD的体积为$\frac{\sqrt{2}}{24}$,直线AB与平面BCD所成角的正弦值为$\frac{\sqrt{3}}{3}$.
三棱锥A-BCD中,△BCD是边长为1的正三角形,点A在平面BCD上的射影为△BCD的中心,E,F分别是BC,BA的中点,EF⊥FD,则三棱锥A-BCD的体积为$\frac{\sqrt{2}}{24}$,直线AB与平面BCD所成角的正弦值为$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图:已知△ABC中,∠BAD=∠C,AB=4,BD=2,$\overrightarrow{BD}$=$\overrightarrow{m}$.
如图:已知△ABC中,∠BAD=∠C,AB=4,BD=2,$\overrightarrow{BD}$=$\overrightarrow{m}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com